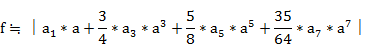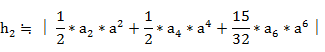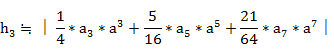|
�������Ȑ�����c�݂��v�Z���� �@from�@�u�I�[�f�B�I�p�^��ǃ}�j���A���v |
��؋g�T����́u�I�[�f�B�I�p�^��ǃ}�j���A���i119�Ł`�j�v�ɁA�c�݂̉��������܂��B�o�͐M�����c��ł��܂��l�q��A���ׂ�^�����������Ȑ�����c�݂����߂������X������A�S�Ă𗝉��ł����킯�ł͂Ȃ��ł����A�ȉ��́A���̕������ł��B
�u�I�[�f�B�I�p�^��ǃ}�j���A��119�Ł`�v�̔���
���ׂ�^����Ec�|Ip�������Ȑ��́A��ʂɑ������ŋߎ��ł���B
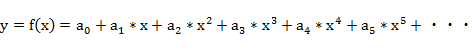
y���v���[�g�d���Ax=�O���b�h�d��
�����ŁAx=a��sin(�� ) �Ƃ���Ɓi �U��=a �̐����g���O���b�h�ɓ��͂����Ƃ��A�o�̓v���[�g�d�� y �� �j
![]()
�ƂȂ�B
�{�p�����ɂ��A�T�C�����̃x�L��͈ȉ���n�{�p�̎��ɕό`�ł���̂ŁA
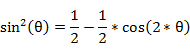
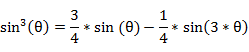
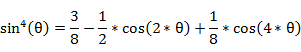
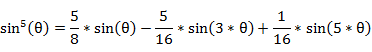
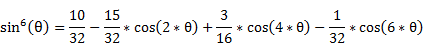
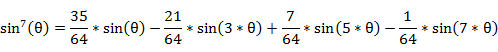
�E�E�E
�@���́A���̂悤��n�{�p�̎��ɕό`�ł���B
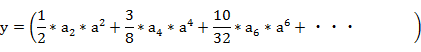
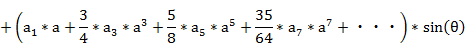
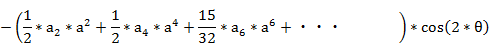
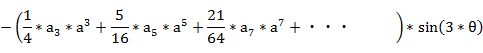
�@�@�@�@�E�E�E
�ȏォ��
�������Ȑ����A���̑������ŋߎ��ł���Ƃ�
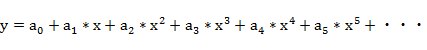
y���v���[�g�d���Ax=�O���b�h�d��
�O���b�h�ɐU��=a �̐����g sin(���j����͂����Ƃ��̃v���[�g�d���̍����g�����͈ȉ��ƂȂ�B
|
���� |
�U�� |
�g�` |
|
��{�g |
|
sin(��) |
|
2�������g |
|
-cos(2*��) |
|
3�������g |
|
-sin(3*��) |
����ɂ��A2���Ђ��݁A3���Ђ��݂́A
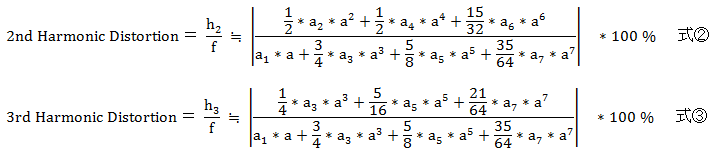
�ƂȂ�B
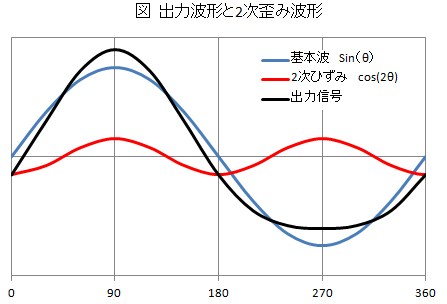
�Ђ��ݐ����̔g�`
�^��ǃA���v�̂Ђ��݂̉���̂Ȃ��ɁA�u�o�͐M���̊�{�g�� sin (��) �Ƃ����ꍇ�A2���c�݂̔g�`�� cos(2*���j�A3���c�݂̔g�`�� sin (3*��)�ƂȂ�v�A�Ƃ�������������܂����B���� 2���c�݂̔g�`��sin(2*���j�ł͂Ȃ��̂�������Ƌ^�₾�����̂ł����A���R���������C�ɂȂ�܂����B
�G�N�Z�����g���ă��[�h���C������c�ݗ����v�Z����
�������Ȑ��̓��[�h���C�����狁�߂��܂��B�܂��A�G�N�Z�����g���ƁA�������Ȑ���̃f�[�^����ߎ��������̊e�W�������߂邱�Ƃ��ł��܂��B�Ƃ������Ƃ́A�G�N�Z�����g���ƁA���[�h���C������c�ݗ����e�ՂɌv�Z�ł���A�Ƃ������ƂɂȂ�܂��B
���ӂ���_�Ƃ��ẮA
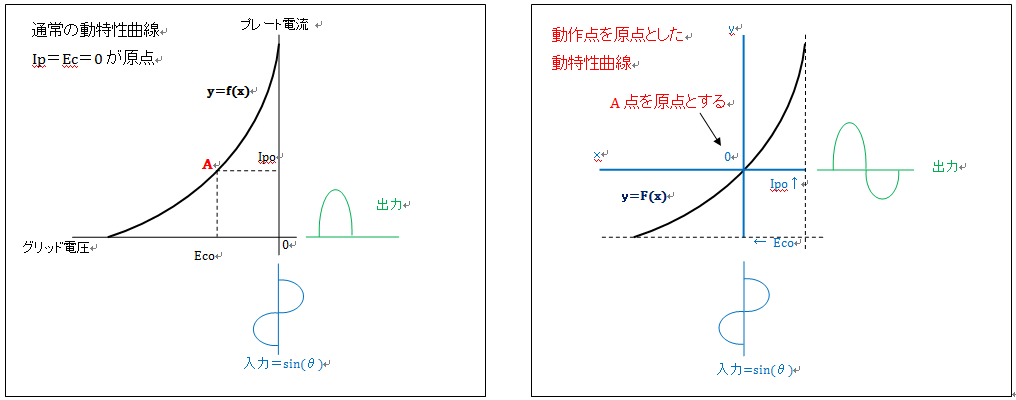
�������Ȑ��̌��_�́A�����̃O���b�h�d����0V�A�c���̃v���[�g�d����0mA�Ƃ��Ă��܂��B���̍��W���̂܂܂œ������Ȑ��̋ߎ������������߁A�w ���͐M�� x=a*sin(��) �Ƃ���Ɓx�A�O���b�h�d����0V ����_�Ƃ��ĐM������͂����Ƃ��́i�o�C�A�X=0V �̂Ƃ��́j�c�݂��v�Z���邱�ƂɂȂ��Ă��܂��A����_����_�Ƃ����ꍇ�̘c�݂ƂȂ�܂���B�����ŁA����_A�i�O���b�h�d��Eco�A�v���[�g�d��Ipo�j�����_�Ƃ����V���ȍ��W����ŁA�������Ȑ���\���K�v������܂��B
|
|
�c�ݗ�������
���ꂩ�烍�[�h���C������c�ݗ����v�Z���Ă݂܂����A�v�Z�œ���ꂽ�c�ݗ��̐��x���m�F���邽�߁A�܂��A�c�ݗ����������Ă����܂��B�����ƌ����Ă��A�V�~�����[�^ Tina7 ���g�����V�~�����[�V��������ł��B�i Tina7 �ɂ̓t�[���G��͂̋@�\������A��{�g�An�������g�̐U���̎����l������ł��܂��B�j
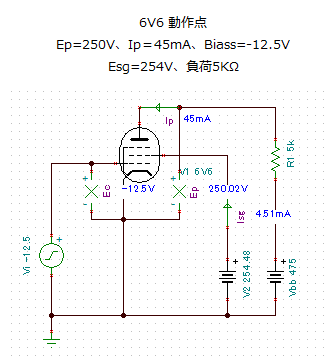
�Ώې^��ǂ�6V6 �Ƃ��A�^��ǃ}�j���A���ɋL�ڂ���Ă��铮���ɍ��킹�āA���ׂ� 5K�� �A����_��Ep=250V�AIp=45mA�ABiass=�|12.5V �Ƃ��܂����B�܂��ATina7 ��6V6 �^��ǃ��f���ł͐^��ǃ}�j���A���̓���Ƃ͎���ق�����A�X�N���[���O���b�h�d�����A�^��ǃ}�j���A���ɋL�ڂ���Ă���250V��荂�߂�254.48V�Ƃ����Ƃ���ŁA���v�̓d��������܂����B
�@�@�@ �@�@�@�@�@
�@�@�@�@�@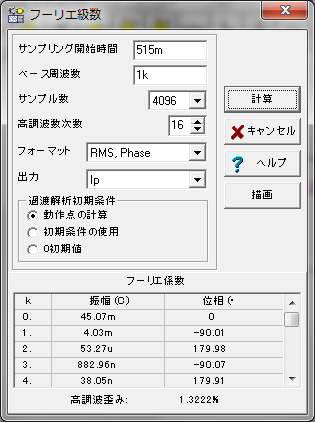
���̑����H�œ��͐M�� Vi�i�����g�j�̑傫���� 12.5V ���� 1.5 V�iVpeak�j�܂ŕω������A���ꂼ��̓��͓d���ɑ��āA�v���[�g�d���̃t�[���G��͂��s���A��{�g�A2�������g�A3�������g�����߂܂����B���ʂ��A�ȉ��ɂ܂Ƃ߂܂��B���L�̉E�}�́A�U�z�}�̋@�\���g���ĕ`�������͓d���ɑ���c�ݗ��O���t�ł��B
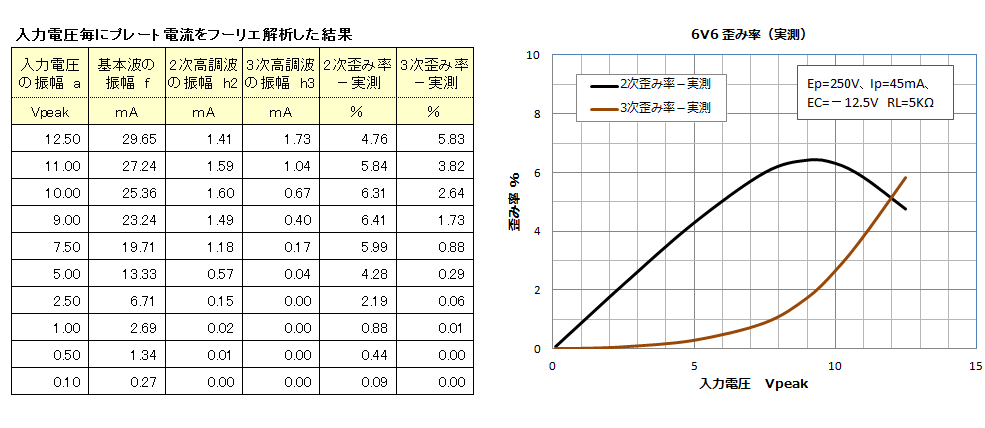
�ł́A���ԂɃ��[�h���C������c�ݗ����v�Z���Ă݂܂��B
�P�j���[�h���C����̊e�O���b�h�d���ƑΉ�����v���[�g�d���̒l�� Ep-Ip �Ȑ����狁�߂܂��B�i ���̂�����̏ڂ������ߕ��́A�u ���[�h���C�����T�N�T�N���� �v���Q�Ƃ��ĉ������B�j
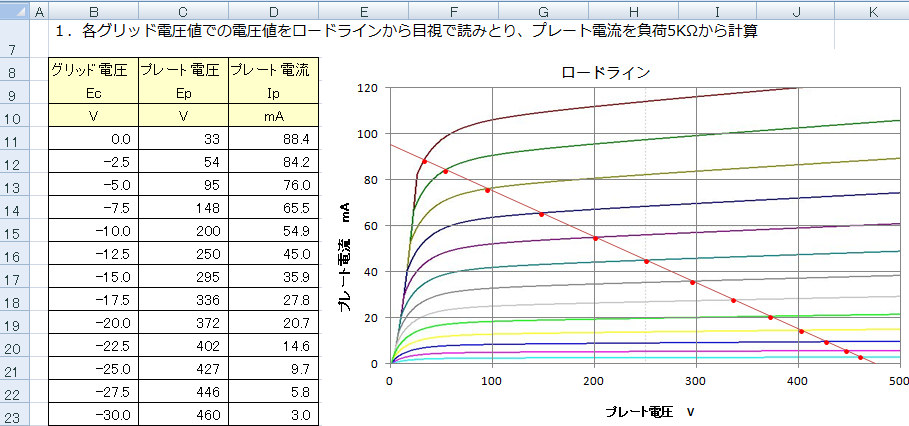
�Q�j���߂��O���b�h�d���ƃv���[�g�d������A����_�̃v���[�g�d���i45mA�j�A�O���b�h�d���i�|12.5V�j�������Z���āA����_�����_�Ƃ����������Ȑ���̃f�[�^�ɕϊ����A���̃f�[�^���瓮�����Ȑ��̋ߎ�5���������̊e�W����LINEST�����g���ċ��߁AINDEX���ŃZ���ɔz�u���܂��B
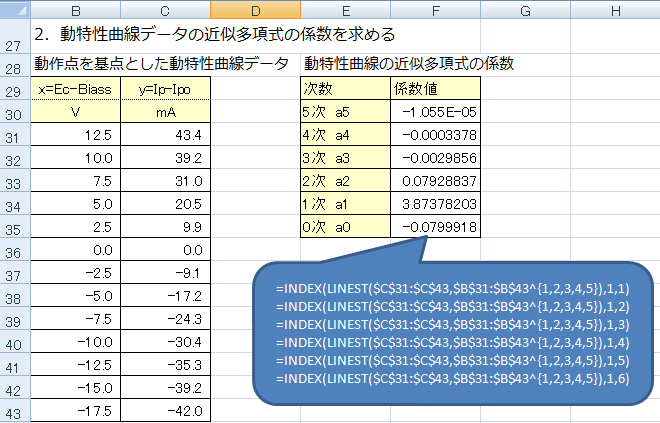
�R�j���A�A���B�ɁA����ꂽ�������̊e�W���Ă͂߂�ƁA���͐M���i�����g�j�̓d���U�� a �ɑ���c�ݗ����v�Z�ł��܂��B���͐M���i�����g�j�̓d���U�� a �̑傫���� 12.5V ���� 0.1 V�iVpeak�j�܂ŕω������A���ꂼ��̘c�ݗ����v�Z���܂����B���L�̉E�}�́A�U�z�}�̋@�\���g���ĕ`�������͓d���ɑ���c�ݗ��O���t�ł��B
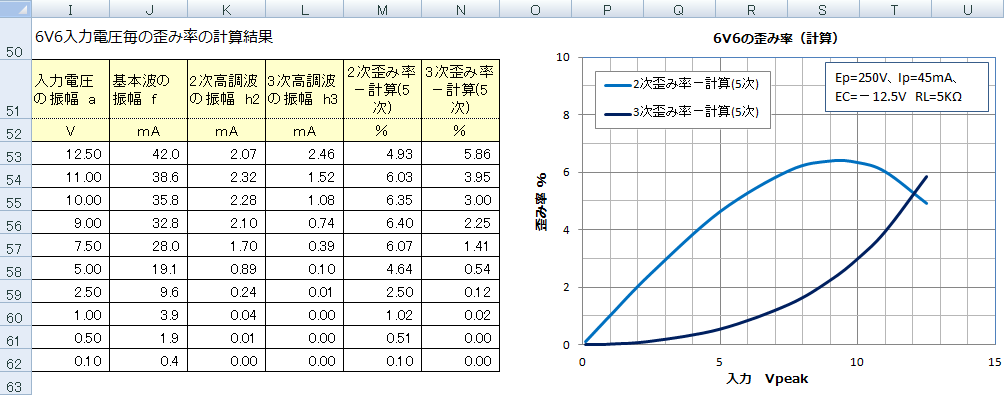
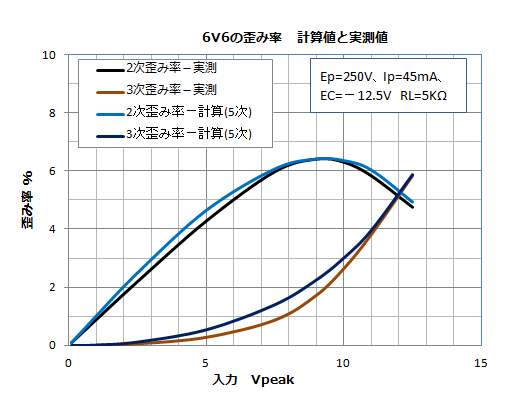
�v�Z���ʂƎ����l�̔�r
���̂悤�ɂ��ă��[�h���C������A���A�B�����g���Čv�Z�ŋ��߂��c�ݗ��Ǝ��������c�ݗ����ׂĂ݂܂����B�ǂ��ł��傤���H���Ȃ肢���������Ⴀ��܂��H
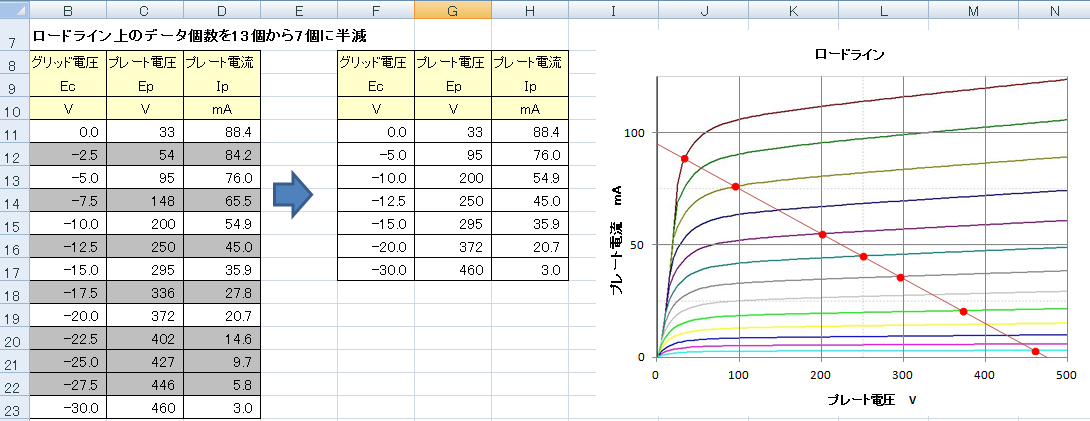
�O���b�h�d�����̃f�[�^��
��� 6V6 �̘c�ݗ��̎Z�o�ł̓O���b�h�d���� 0V����|30V�܂ł́A2.5V�X�e�b�v��13�̃f�[�^���g���v�Z���܂������A�v���[�g�����}���瓾����O���b�h�d�����̃v���[�g�d���̃f�[�^���́A���ۂ͂���قǑ����͂���܂���B���ɑ��Ɋǂ̏ꍇ�́A6����8���炢�ł��傤���B
�ߎ��������̐��x�̓f�[�^�̌��Ɉˑ����܂��B�f�[�^�������Ȃ��ꍇ�͂ǂ̒��x�̐��x�_�E���ɂȂ�̂��A13�̃f�[�^���Ԉ�������7�܂Ō��炵�A�c�ݗ����v�Z���Ă݂܂����B
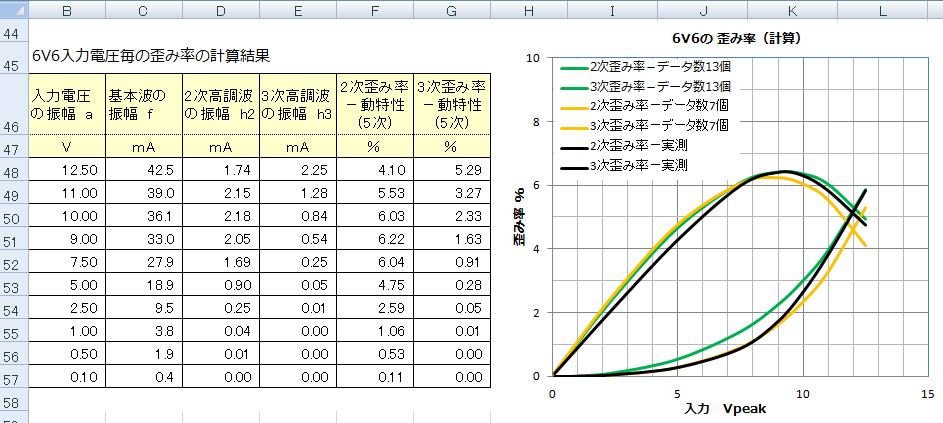
����ꂽ�c�ݗ��͈ȉ��̂Ƃ���ł��B���F�����V�̃f�[�^�A�ΐ���13�̃f�[�^�Ōv�Z�������ʂł��B13�̂Ƃ��������l�Ƃ̍��ق͑傫���Ȃ��Ă��܂����A2���c�݂ł̏����͎��͎����ɂ��߂��l�Ă��܂��B
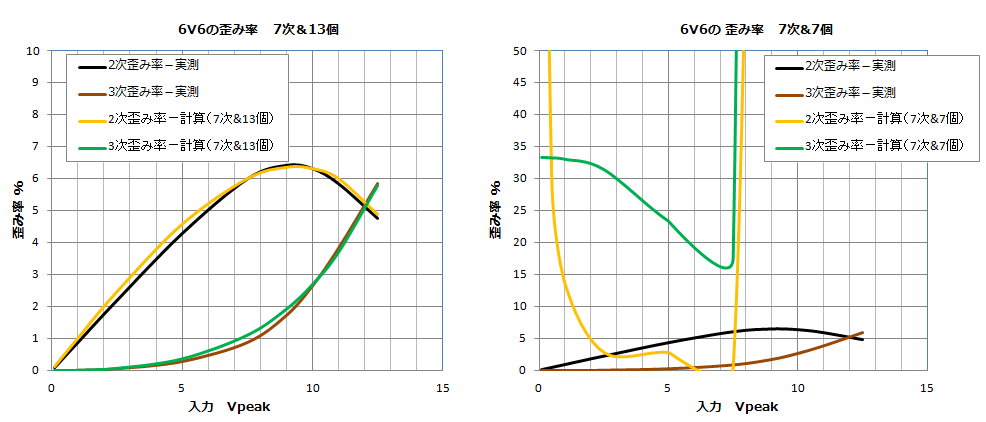
7����������5��������
��� 6V6 �̘c�ݗ��̌v�Z�ł� �������̎����� 5 ���Ƃ��܂����B������@�� 7 ���̑������ł����߂Ă݂܂��B�f�[�^�̌��́A���5���̑������ł̌v�Z�Ɠ��l��13�̏ꍇ�� 7�̏ꍇ��2��ނƂ��܂����B
13�ƃf�[�^���������Ƃ������ɋ߂��Ȃ�܂������A7�̏ꍇ�͂܂������g���Ȃ����ʂƂȂ�܂����B����́A�ߎ������������߂�Ƃ��f�[�^�̌������Ȃ��ƁA�f�[�^�̊Ԋu���ɂ�葽�����̎��������� 7 ���̕��� 5 �������������Ď��ԂƂ̍������߂ɎZ�o����Ă��܂����Ƃ��v�����Ǝv���܂��B
���̐^��ǂł́H
�G�N�Z���̃V�[�g�����܂����B�����̂�����͂ǂ����B���̃V�[�g���g���A�������̐^��ǂŌv�Z���Ă݂܂����B
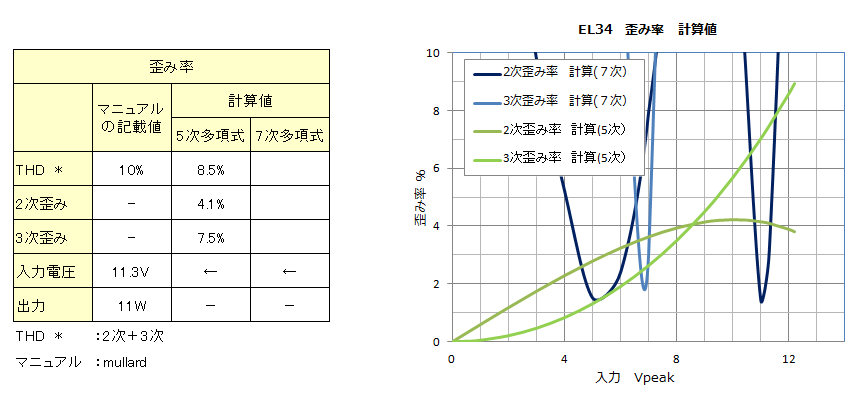
![]() EL34�@�E�E�E�@�}�j���A���ɋL�ڂ�Ă���c�ݗ��Ɣ�ׂāA�v�Z�ŋ��߂����ʂ́A5 ���̑������ł͎�Ⴂ�c�ݗ��ɂȂ�܂����B�܂��A7���̑������ł͗ǂ����ʂ������܂���ł����B
EL34�@�E�E�E�@�}�j���A���ɋL�ڂ�Ă���c�ݗ��Ɣ�ׂāA�v�Z�ŋ��߂����ʂ́A5 ���̑������ł͎�Ⴂ�c�ݗ��ɂȂ�܂����B�܂��A7���̑������ł͗ǂ����ʂ������܂���ł����B
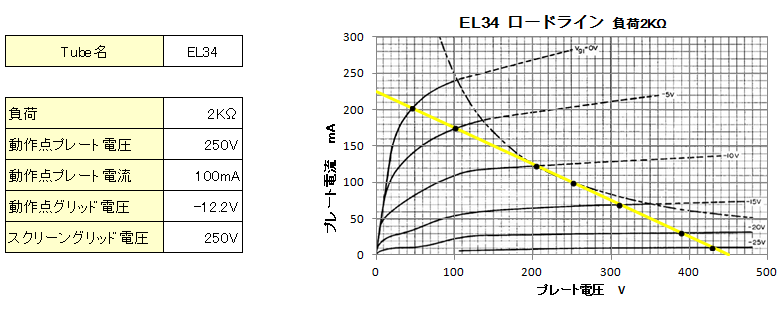
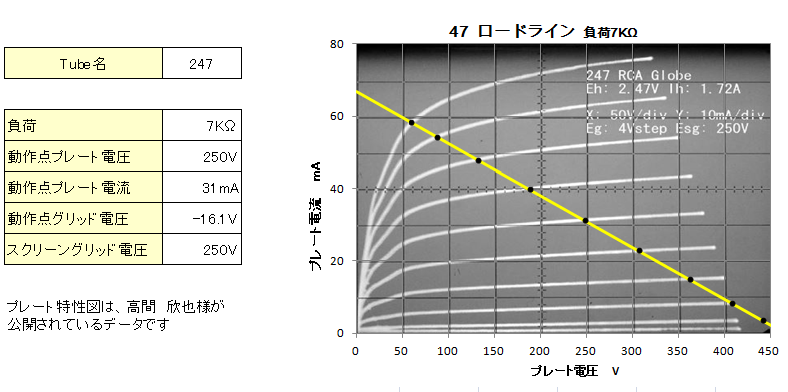
![]() 47�@�E�E�E�@�v���[�g�����}�́A�C���^�[�l�b�g��ő����� EP-IP �����f�[�^�����J�u Ep-Ip
Curve�f�[�^�W�i2006�N7��15���j�v���Ă����鍂�ԋӖ�l�̃f�[�^���g�킹�Ă��������܂����B���̂悤�ȗL�v�ȃf�[�^�𑪒肵���J���ꂽ���ԗl�Ɋ��ӂ������܂��B
47�@�E�E�E�@�v���[�g�����}�́A�C���^�[�l�b�g��ő����� EP-IP �����f�[�^�����J�u Ep-Ip
Curve�f�[�^�W�i2006�N7��15���j�v���Ă����鍂�ԋӖ�l�̃f�[�^���g�킹�Ă��������܂����B���̂悤�ȗL�v�ȃf�[�^�𑪒肵���J���ꂽ���ԗl�Ɋ��ӂ������܂��B
�v�Z���ʂ́ACunningham�Ђ̐^��ǃ}�j���A���̒l�ɋ߂��l�ƂȂ�܂����B
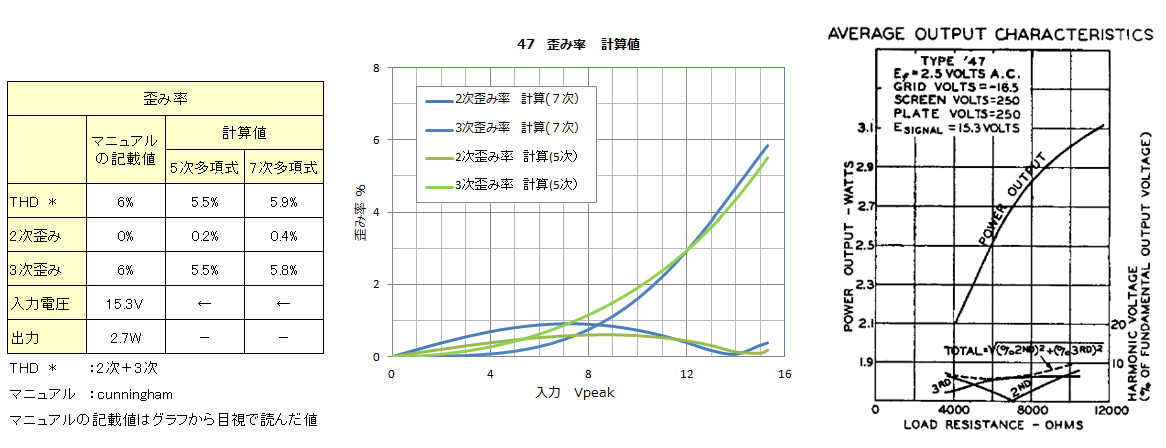
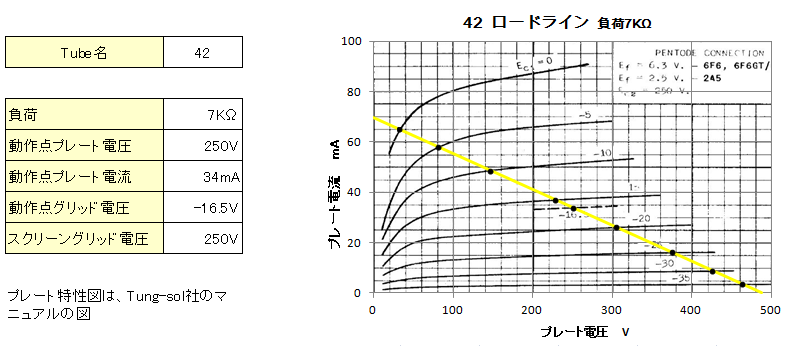
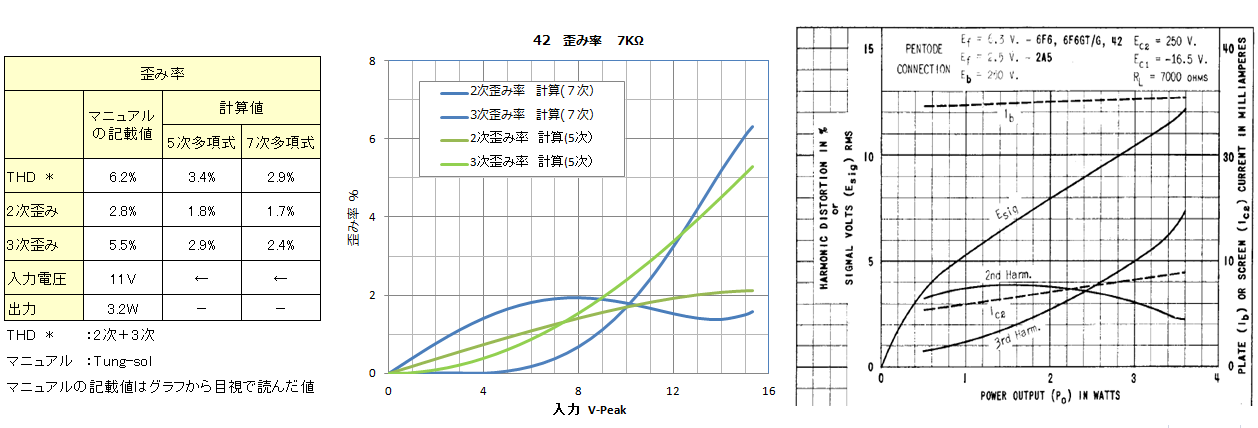
![]() 42 �E�E�E�@Tung-sol�̃}�j���A���ɋL�ڂ���Ă���c�ݗ��Ɣ�ׂāA�v�Z�����c�ݗ��͂����Ԃ�Ⴂ�l�ƂȂ�܂����B�c�ݗ��Ȑ��̌`��7���������ł̌v�Z���ʂ�����Ȃ�H�ł��傤���B
42 �E�E�E�@Tung-sol�̃}�j���A���ɋL�ڂ���Ă���c�ݗ��Ɣ�ׂāA�v�Z�����c�ݗ��͂����Ԃ�Ⴂ�l�ƂȂ�܂����B�c�ݗ��Ȑ��̌`��7���������ł̌v�Z���ʂ�����Ȃ�H�ł��傤���B
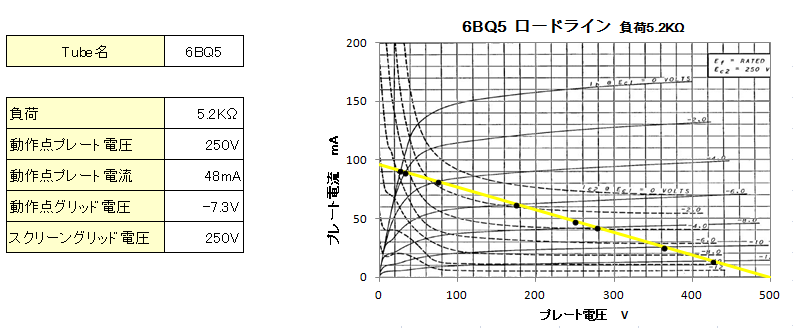
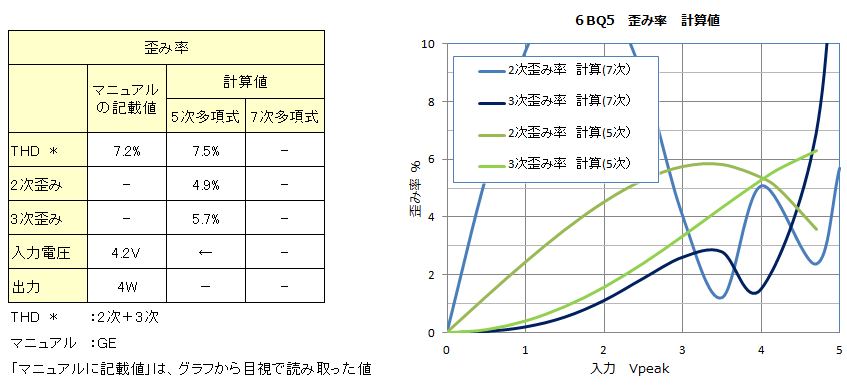
![]() 6BQ5�@�E�E�E�@�}�j���A���ɋL�ڂ�Ă���c�ݗ��Ɣ�ׂāA�v�Z�ŋ��߂����ʂ́A5 ���̑������ł͎�Ⴂ�c�ݗ��ɂȂ�܂����B�܂��A7���̑������ł͗ǂ����ʂ������܂���ł����B
6BQ5�@�E�E�E�@�}�j���A���ɋL�ڂ�Ă���c�ݗ��Ɣ�ׂāA�v�Z�ŋ��߂����ʂ́A5 ���̑������ł͎�Ⴂ�c�ݗ��ɂȂ�܂����B�܂��A7���̑������ł͗ǂ����ʂ������܂���ł����B
�Q�l���ЁA�Q�l�z�[���y�[�W
¬ ��؋g�T���@�w�I�[�f�B�I�p�^��ǃ}�j���A���x�@���W�I�Z�p��
¬ ���ԋӖ�l�@�u Ep-Ip Curve�f�[�^�W�i2006�N7��15���j�v�@������ EP-IP �����f�[�^
�uKAKUSAN�^��ǃA���v�v�֖߂�@�@�@�u���̕ł̃g�b�v�v�֖߂�