「情熱の真空管アンプ」のおかげでロードラインがひけるようになりました。プレート特性図を眺めながらあれこれとヒッパッテみて妄想するのは結構楽しい時間です。
ただ、例えば、下図は EL34 のロードラインですが、プレート電流が100mAでプレート電圧が250VのA点のグリッド電圧を精度よく読み取るには、結構難しい。
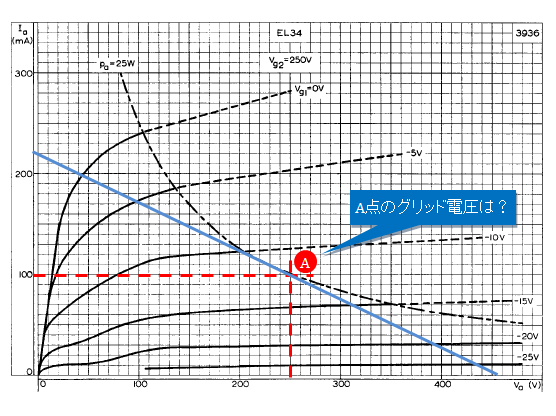
なんとか、サクサクっといかないものか？ と思っていたところ、動特性曲線とエクセルの近似多項式の機能を活用すると、所望のグリッド電圧やプレート電流の値を簡単に計算できることが判りました。
以下に、この活用手法をまとめました。
動特性曲線
一木吉典著『真空管マニュアル』によれば、プレートに負荷を与えた真空管のグリッド電圧Ecとプレート電流 Ip の関係を表した曲線を動特性曲線と呼ぶそうです。
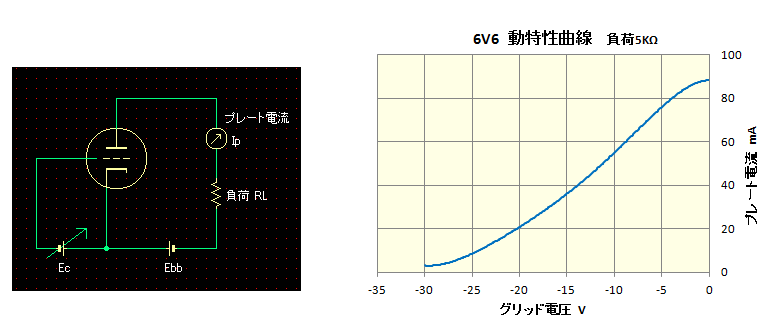
ロードラインは、プレートに負荷を与えた真空管のプレート電圧 Epとプレート電流 Ip の関係を表しています。
したがって、プレートに負荷を与えた真空管のグリッド電圧 Ec、プレート電流 Ip、プレート電圧 Ep の3つの要素の関係を表した動作データのうち、縦軸を Ip、横軸を Ecとしてプロットすれば 動特性曲線となり、 縦軸を Ip、横軸を Ep としてプロットすれば ロードラインとなります。
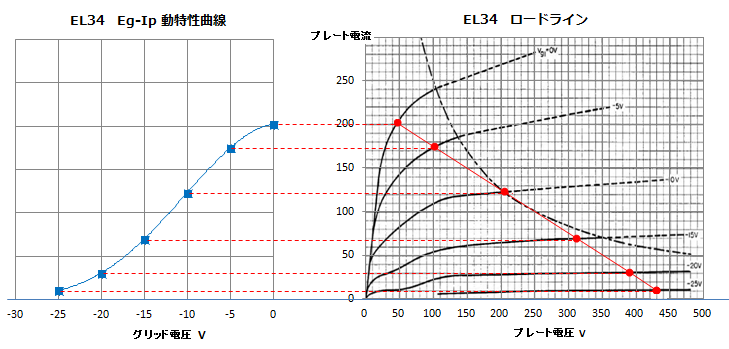
また、エクセルには、ｘ とｙ の関係を示したデータ群からｙ＝ｆ(ｘ）の近似多項式を得る機能がありますので、ロードライン上の何点かのグリッド電圧 Ec とプレート電流 Ip の動作データがあれば、Ip から Ec を得る近似多項式 Ec＝ｆ(Ip）を求めることができます。この近似関数を使えば、ロードライン上の任意の点Ａにおけるグリッド電圧は、Ａ点のプレート電流から計算して求めることができます。
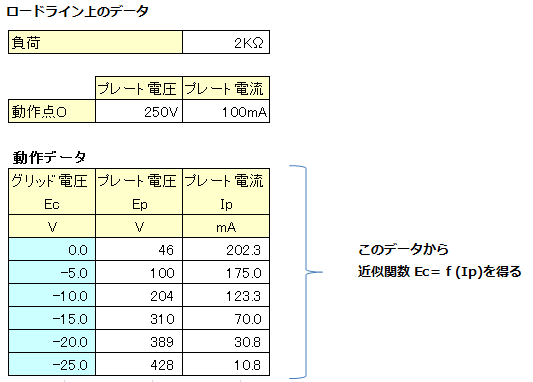
動特性曲線の近似多項式によるグリッド電圧とプレート電流の計算方法
前準備
真空管マニュアルのプレート特性図から、必要となる電圧と電流の範囲を Windows のおまけのソフト『 Snipping Tool 』などを使って切り出して、図形として保存する。
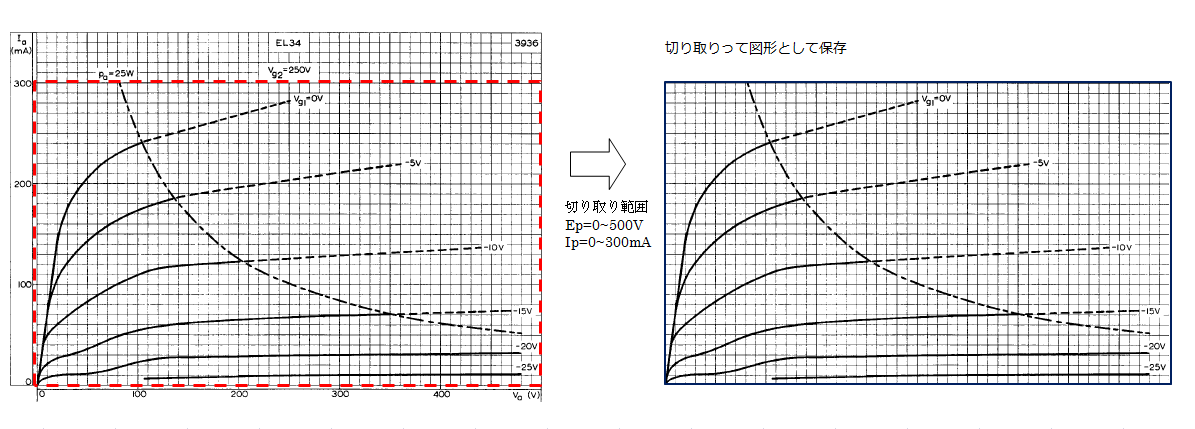
ワンポイント ：Webで公開されている特性図は、若干斜めになっていることが多い。 フリーグラフィックソフト『 GIMP 』は、100分1度の精度で図形を回転させることができるのでこの傾きの補正が可能です。ただ、斜めの度合いは、真空管の個体差やスピーカー負荷の変動に比べたら、誤差の範囲で気にするほどのことは無いのかもしれません。
ロードライン上の動作データを目視で読み取り
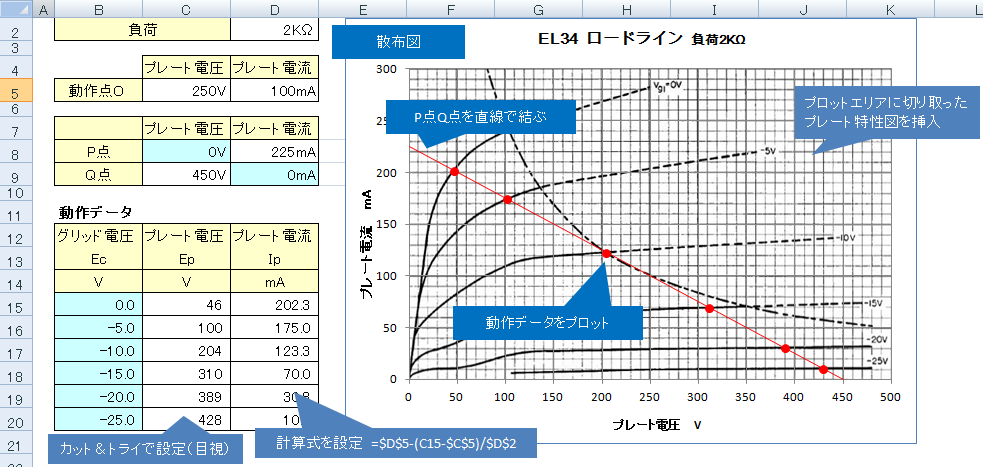
1. 動作点O (プレート電圧Epo、プレート電流Ipo）と負荷 RL を決め、プレート電圧＝０Vとなる点（P点）、プレート電流＝0mAとなる点（Q点）の座標を計算で求める。
2. 次いで、グラフ（散布図）機能により、P点からQ点を結ぶロードラインを描く。プロットエリアには前準備で切り取ったプレート特性図の図形を挿入する。
3. 各 Ep−Ip曲線とロードラインの交点における、グリッド電圧Ec、プレート電圧Ep、プレート電流Ipを要素とした動作データを作成する。
¬ 動作データを2で作成したグラフにプロットする。
¬ Ip値は、計算式とする。 Ip＝Ipo ＋（Ep−Epo）/ RL
¬ Ep値は、プロットした点が、対応するEp−Ip曲線とロードラインの交点とぴったりと重なるよう、目視によりカット＆トライで求める。
動特性曲線の近似多項式により所要のグリッド電圧やプレート電流を求める。
エクセルには、グラフのデータ系列に対する多項式近似曲線の係数を得る機能があります。関数LI NESTです。
例えば、xの値がA2〜A10セルに、それぞれに対応するyの値がB2〜B10セルに配列されており、このxとyの関係を
で近似させた場合、
係数a0、a1、a2、a3は
a1=INDEX(LINEST(B2:B10,A2:A10^{1,2,3}),1,1)
a2=INDEX(LINEST(B2:B10,A2:A10^{1,2,3}),1,2)
a3=INDEX(LINEST(B2:B10,A2:A10^{1,2,3}),1,3)
a0=INDEX(LINEST(B2:B10,A2:A10^{1,2,3}),1,4)
という数式で求まるそうです。
このLINEST関数を使って動特性曲線の関係式を求めます。下記は、プレート電流とグリッド電圧の動作データを、5次の多項式で近似したときの各係数の値をLI NEST関数で求め、INDEX関数でG列に配値したシート例です。簡単ですね。
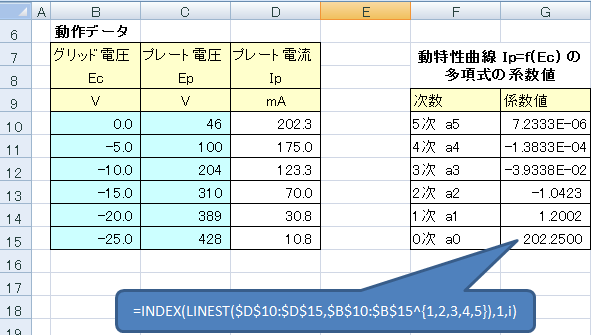
こうして求めた近似多項式のIp＝ｆ(Ec)を使って、Ec 値から Ip 値を計算することができます。下記は、プレート電流からグリッド電圧を表計算させるシート例で、プレート電流が100mA のときのグリッド電圧は−12.2V と自動計算できました。
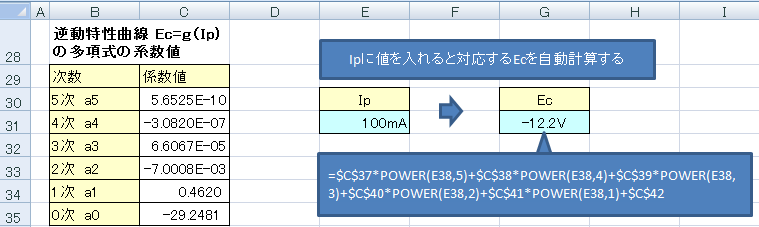
同様にグリッド電圧から、プレート電流を自動計算させることもできます。
精度と限界
近似多項式の次数と精度
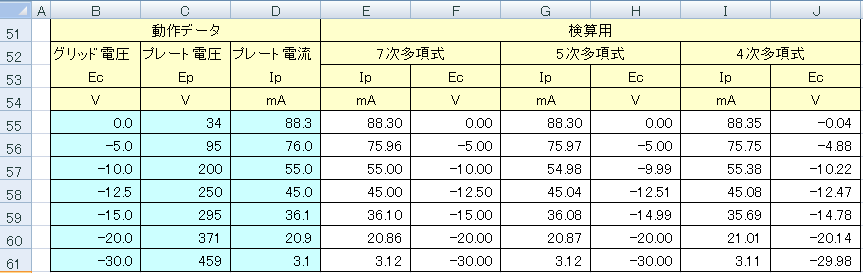
近似多項式の次数を、4次、5次、7次で計算した結果と元の値を比較してみました。
下記の「検算用」と記された列が近似多項式で、グリッド電圧からプレート電流を、また、プレート電流からグリッド電流を計算した値です。このように元の動作データ点と計算した値とは、さほどの差異はありませんでした。
次に動作データ点間の精度を確認してみます。
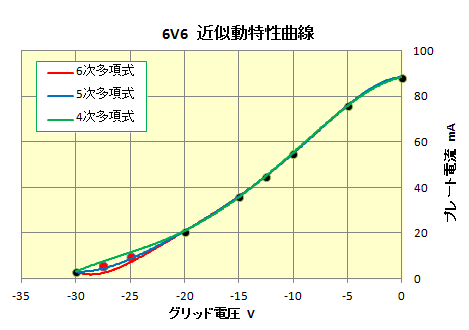
下記は、6V6 の動特性曲線の多項式近似曲線で、次数は、4 次、5 次、6 次です。黒丸が近似曲線を求める際に使った動作データで、Ec=0V、−5V、−10V、−12.5V、−15V、−20V、−30Vの 7 ポイントです。赤丸は、比較のためわざと使用しなかった動作データで、Ecは−25Vと−27.5Vです。動作データは、シミュレータ Tina7 で回路を作成して測定した値です。
プロットした動作データは7個とそこそこの個数ですが、EC＝−20Vと−30Vの間は、4 次、5次、6次 の近似曲線でかなり差が出ました。また、次数が高いほど精度が上がる、とは言えない結果でした。
このように、特に動作データの最終区間が長い場合は、むやみに次数を上げないほうが良さそうです。ロードラインから得られるデータでは、5次くらいが妥当かと思います。
この手法の限界
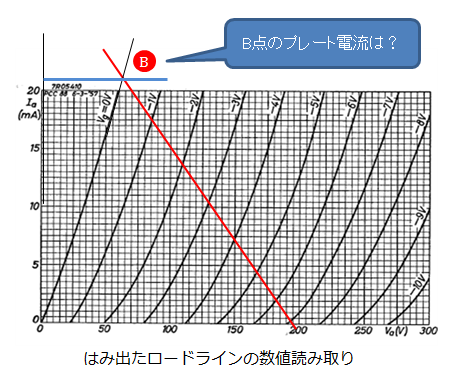
下記の B 点のように、プレート特性図からはみ出したポイントでのプレート電流を求めたいことがあります。B 点は、得られる動作データの範囲外にありますが、B点の電流値をこの動特性曲線の近似多項式により計算したところ、誤差が多いことが判りました。
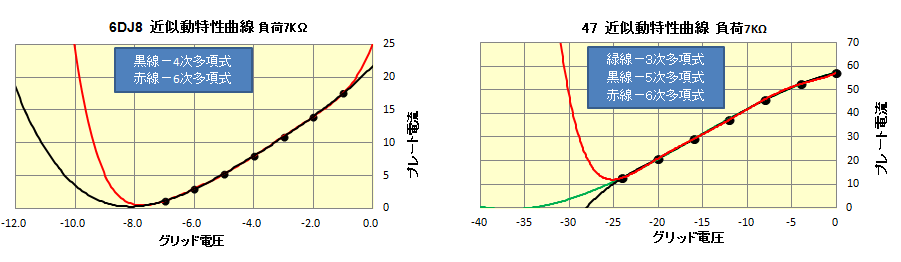
下図は、2 ヶの真空管 6DJ8 と 47 の動特性曲線の多項式近似曲線です。黒丸がプロットした動作データです。
得られる動作データ値の外側では、困った曲線になっています。しかも、次数が高いほど困った度合いが高くなっています。
理由は良く判りませんが、動特性曲線の動作データの近似多項式により Ec、Ip を計算する手法は、B 点のような動作データ値の外側の値を計算させると、誤差が多く出てしまい無理があるようです。
近似のメカニズムまでは勉強がいたらず、近似多項式の精度が不透明です。また、そもそも動特性曲線の近似式として多項式がフィットする理由は不明です。
この手法の理屈は判りませんが、限界を意識すれば、ロードラインを引く際には便利なツールかと思います。以下、ご参考までに、作成したエクセルのワークシートをアップしておきます。
参考書籍
¬ 一木吉典著 『オーディオ用真空管マニュアル』 ラジオ技術社
「KAKUSAN真空管アンプ」へ戻る 「この頁のトップ」へ戻る