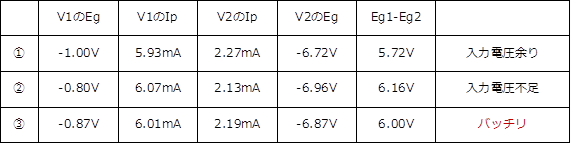片側入力の差動回路－ロードライン

Ver.01 2014/12/8

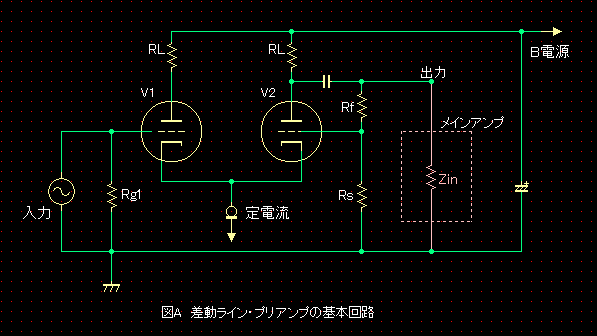
片側入力の差動回路の左右の真空管V1、V2は、どのような傾きのロードラインで動作をしているのでしょうか？また、どのような連携をしているのでしょうか。Ep-Ip特性図から負荷の大きさを求めて、ロードラインを引いてみました。

回路定数

ぺるけさんの記事（旧版）では、真空管は6DJ8を筆頭に使用できる真空管がいくつも紹介されています。回路のトレース／シミュレーションにあたって、本項では、6DJ8と12AU7を使用します。回路定数は、6DJ8と12AU7で同じ値を適用することにして、記事に準拠し、直流負荷RL=20KΩ、負帰還抵抗を100KΩと56KΩ、Ip＝4.1mA、B電圧＝203V、また、メインアンプの入力インピーダンスを50KΩとおきました。この定数での12AU7の動作点・三定数は、下表となります。（ TINA7-BOOK3の真空管モデルの値です。）

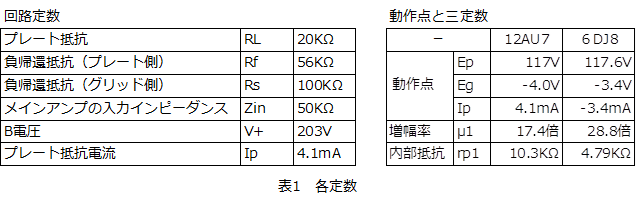
P-G帰還無しのときの負荷

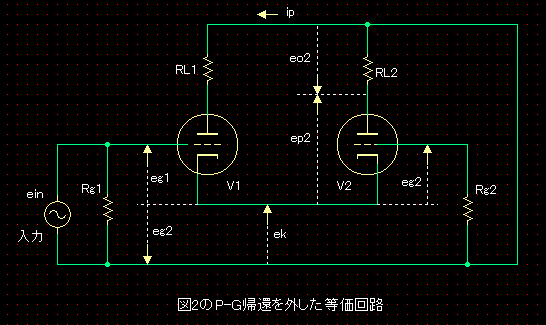
図1の回路からP-G帰還をはずした（RfとRsは残しV2のグリッドをRg2を経由してグランドへ落とした）うえで、電源はショート、コンデンサーはショート、定電流はオープン、として等価回路を描いてみました。図2です。RL1=RL、RL2＝RL//(Rs+Rf)//Zin　とし、また、信号einが入力されたときの、各交流信号、V1とV2のグリッド電圧、カソード電圧、プレート電圧、プレート電流、出力を、eg1、eg2、ek、ep2、ip、eo2としています。

この図2から、Rg2には電流は流れていないので、eg2は、ekの反数となることが分かります。また、入力信号einは、V1のグリッドとV2グリッドの間に入力されていることが分かります。従い、以下が成り立ちます。

eg1=ein－ek　・・・　①-1

eg2=－ek 　　・・・　①-2

また、プレート電圧ep2、出力eo2、カソード電圧ek、及び、プレート電流の間には、次の関係が成り立っています。

ep2＝eo2－ek

eo2=ip＊RL2

この2式から、V2の負荷Rp2は、Rp2＝ep2／ip＝(eo2－ek)／ip＝RL2－ek／ip　・・・　②

従って、V2の負荷Rp2＝ep2/ipは、RL2よりek/ipだけ小さいはずです。

同様に、V1の負荷Rp1＝ep1/ipは、RL1よりek/ipだけ大きいはずです。

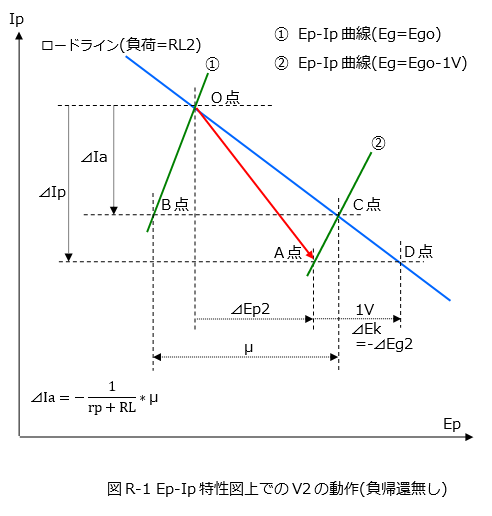
V2の負荷Rp2が具体的にどの程度RL2より小さいのか、Ep-Ip特性図上で作図により求めてみます。図R-1は、Ep-Ip特性図上での回路図2（無負帰還）のV2の動作です。

緑線①と②は、Ep-Ip曲線です。①はバイアスがEgo[V]、②はバイアスが①より1V少ないEgo-1[V]です。O点がV2の動作点（Eg=Ego）で、青線はO点を通過する負荷RL2のロードラインです。

いま、入力信号を与えたとき、V2のグリッド電圧が1Vだけ減少したとします。(⊿Eg2=－1V)

このとき

² V2は、O点から、バイアスがEgo-1[V]のEp-Ip曲線②上のどこかに移動するはずです。この移動後の点をA点とし、プレート電流の変化量を⊿Ipとします。

² 青線のロードライン上で、O点よりプレート電流が⊿Ipだけ少なくなったときの点をD点とすると、A点の電圧は、D点よりカソード電圧の増加分⊿Ekだけ少ないはずです。（②式より）

² カソード電圧の増加分は、⊿Ek=－⊿Eg2＝1Vのはずです。(①-2式より）

従い、赤線の傾きは、緑線の傾きRL2より、⊿Ek/⊿Ip=1/⊿Ipだけ小さくなるはずです。

1/⊿Ipを求めると、

・三角形CADは、三角形OCBと相似で、その長さの比は、１：μ2

従い、P-G帰還無しのとき（図2の回路）

ここで、rp2はV2の内部抵抗、μ2は、V2の増幅率

となりました。

参考）ロードラインと三常数

基本回路（図１）の負荷

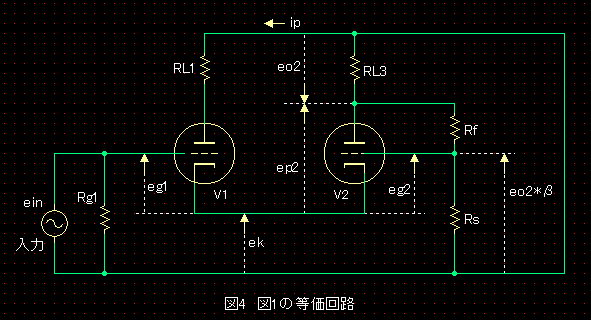
基本回路（図1）の、電源をショート、コンデンサーをショート、定電流源をオープン、として等価回路を描いてみました。図4です。RL1=RL、RL3＝RL//Zin　としています。

注）各電圧、電流値は、図2と記号は同じですが値は異なります。

負帰還電圧はV2のグリッドに印加されています。従い、V2のグリッド電圧は、カソード電圧から負帰還電圧が減算された値の反数となりますので、次の関係が成り立ちます。

eg1=ein－ek　・・・　①-1

eg2=β*eo2 －ek 　　・・・　①-2

ここで、β=Rs／(Rs+Rf)

また、プレート電圧ep2、出力eo2、カソード電圧ek、及び、プレート電流の間には、次の関係が成り立っています。この関係は、P-G帰還をかけない回路と同じでした。

ep2＝eo2－ek

eo2=ip＊RL2

この2式から、V2の負荷Rp2は、Rp2＝ep2／ip＝(eo2－ek)／ip＝RL2－ek／ip　・・・　②

従って、V2の負荷Rp2＝ep2/ipは、RL2よりek/ipだけ小さいはずです。

同様に、V1の負荷Rp1=ep1/ipは、RL1よりek/ipだけ大きいはずです。

注）RL2＝RL3//(Rf+Rs)=RL//(Rf+Rs)//Zin　です。

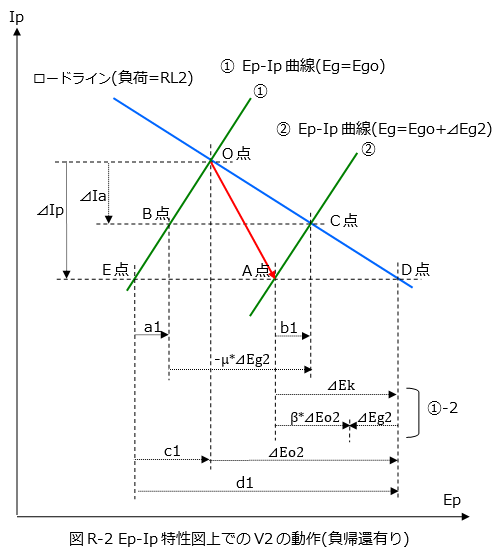
V2の負荷ep2/ipが具体的にどの程度RL2より小さいのか、Ep-Ip特性図上で作図により求めてみます。

図R-2は、Ep-Ip特性図上での基本回路（図1）のV2の動作です。緑線①と②は、Ep-Ip曲線です。①はバイアスがEgo[V]、②はバイアスが①より⊿Eg2[V]少ないEgo-⊿Eg2[V]です。O点がV2の動作点（Eg=Ego）で、青線はO点を通過する負荷RL2のロードラインです。

いま、入力信号を与えたときV2のグリッド電圧が⊿Eg2[V]減少したとします（⊿Eg2はマイナス値）。

このとき

² V2は、O点から、バイアスがEgo+⊿Eg2[V]のEp-Ip曲線②上のどこかに移動するはずです。この移動後の点をA点とし、プレート電流の変化量を⊿Ipとします。

² カソード電圧の増加分は、⊿Ek=－⊿Eg2+β*Eo2のはずです。(①-2式より）

従い、赤線の傾きは、緑線の傾きRL2より、⊿Ek/⊿Ipだけ小さくなるはずです。

E点とB点間の電圧a1とA点とC点間電圧b1が等しいのは明らか（＃1）なので、E点とD点間電圧d1は、

従い、図1の基本回路において

ここで、rp2はV2の内部抵抗、μ2は、V2の増幅率

となりました。

（＃1）実際のEp-Ip曲線は平行ではない

（＃2）詳細

ロードラインを引いてみます

V1・V2の負荷を求める数式が得られました。イメージを掴むためにこの数式を用いて12AU7を使った場合のロードラインを引いてみます。回路定数は、表1を使います。

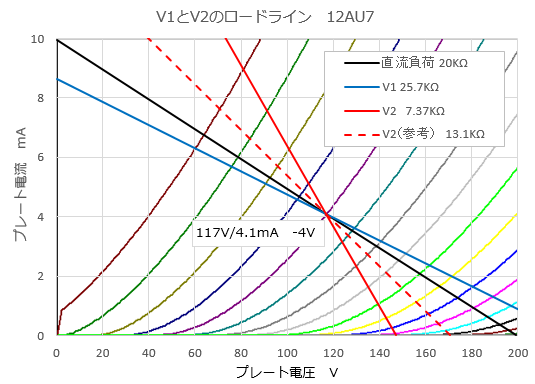
表1の定数で計算した結果、V1の負荷は 25.7KΩ、V2の負荷は 7.37KΩとなりました。

直流負荷RLの20KΩ、また、直流負荷RLと負帰還抵抗とメインアンプの入力インピーダンスの並列合成抵抗値の13.1KΩ（＝20KΩ//156KΩ//50KΩ）と比べて、結構差があるなぁ、と思いました。また、V2のロードラインは、思っていた以上に立っている感じです。

図R-3 V1とV2のロードライン 12AU7

ロードラインは曲線（若干ですが）

内部抵抗rp2と増幅率μ2はプレート電圧やプレート電流に応じて変化するので、ロードラインは直線ではないはずです。どのくらいの曲りの曲線になるのか12AU7を使った基本回路（図1）でシミュレーションしてみました。シミュレーション回路の定数は表1の値です。

赤細線が計算式から得られたRL2=7.37KΩの直線ロードラインで、赤太線がシミュレーションでの動作結果です。1mA以下では曲りが明らかですが、実際に使われる領域ではほぼ直線とみて支障はなさそうでした。直線性のあまり良くない12AU7でこの程度なので、他の球でも同様に直線と見なしても良いかと思います。

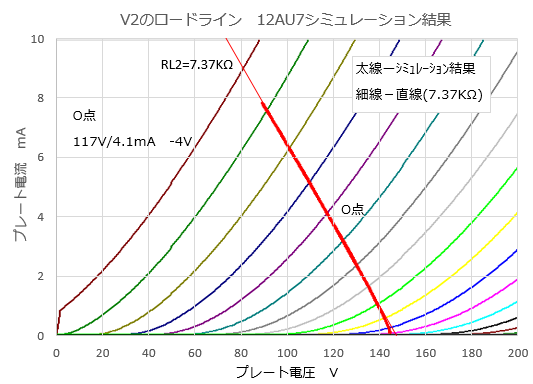
図R-4 V2のロードライン 12AU7シミュレーション結果

ロードライン上での動作

V1とV2の個々の球が2本のロードライン上でどのように動いているのか具体的にトレースしてみます。

トレース回路は、12AU7を使った基本回路（図1）からRsとRfを取り去った負帰還無しの回路です。定数は表1の値で、負帰還無しのときの負荷を計算すると、V1が21.3KΩ、V2が12.9KΩでした。動作点は、Ep=117V、Ip=4.1mA、バイアス=－4Vです。

今、プラス6V（Peak値）の入力信号を与えます。図2から、この入力電圧は分割されてV1とV2のグリッドに入力され、V1のグリッド電圧をプラス方向に、V2をマイナス方向に振ります。従い、ロードライン上、V1は左上方向に移動し、V2は右下方向に移動していきます。

① V1のグリッド電圧が－1Vとなったとします。ロードライン上、バイアスが－1のときV1のプレート電流は5.93mAで、動作点から1.83mAの増加です。V2のプレート電流は同じ量だけ減少するので2.27ｍAとなります。ロードライン上、プレート電流が2.27mAのV2のバイアスは－6.72Vです。従い、グリッドーグリッド間電圧は、＋5.72Vになるので入力電圧（＋6V）がまだ余っています。

② そこで、もう少しV1のグリッド電圧を上げて、－0.8Vとします。このときV1に流れるプレート電流は動作点から1.97mA増えて6.07mAです。V2は、プレート電流が2.13ｍA（1.97mA減）となり、グリッド電圧は－6.96Vになります。従い、グリッドーグリッド電圧間は、＋6.16Vになるので入力電圧（＋6V）が足りません。

③ そこで、今度はもう少しV1のグリッド電圧を下げてみます。－0.87Vです。このときV1に流れるプレート電流は動作点から1.91mA増えて6.01mAです。V2は、プレート電流が2.19ｍA（1.91mA減）となり、グリッド電圧は－6.87Vになります。従い、グリッドーグリッド間電圧は、6Vとなり、入力電圧とピッタリでした。

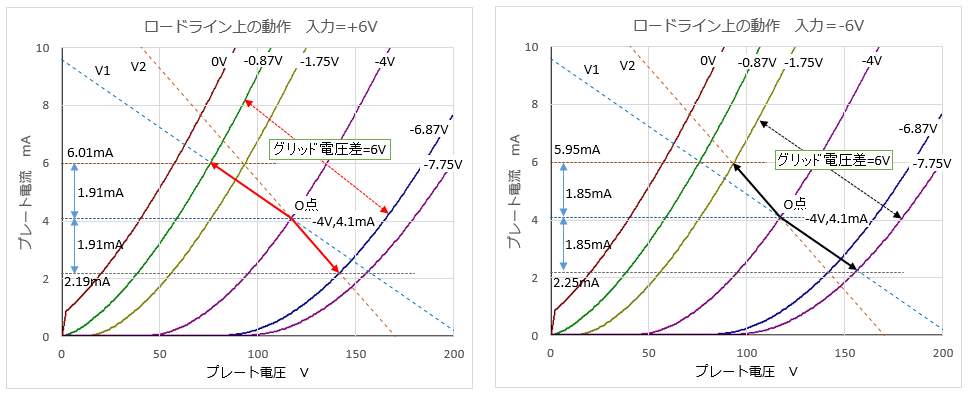
図R-5の左側がプラス６Vの入力を与えたときの動きで、右側がマイナス6Vの入力を与えたときの動きです。青点線がV1のロードライン、赤点線がV2のロードラインです。

図R-5 ロードライン上の動き

入力がプラス6Vのときプレート電流はプラス1.91mA増加し、入力がマイナスのときプレート電流はマイナス1.85mA減少しています。この1.91mAと1.85mAの差は、作図的には、V1とV2とでロードラインが異なることが要因と考えらます。そして、正弦波が入力されたときの出力電圧は、山が高く谷が低くなるので、高調波歪みが発生しているはずです。

このことから、V1とV2が同じロードライン上を動くならば、プレート電流（の絶対値）の差は無く、高調波歪みは発生しなくなるはずです。この想定は、本項の後段で確認してみます。

片側入力の差動回路は、入力電圧を分割してV1とV2に与えますが、適当に分割しているわけでは無く、異なるロードライン上でV1とV2のプレート電流が等しくなるように（向きは逆）塩梅よく分割していることが分かりました。

電気の世界（物理の世界？）では当たり前なのかもしれませんが、先の例のように①や②のような試行はせず、一発でピタリと分割してしまう、そしてさらに負帰還の場合はもっと条件が増えるのですが瞬時に分割して調和してしまう、、、瞬時に複数条件を満たす解を与え調和させ続けるという意味で、なにかすごいなぁと思います。。。。

不思議なこと

通常の回路にP-G帰還を施したときには負荷の大きさは変わりませんでした（「真空管アンプのP-G帰還」）。しかし、この片側入力の差動回路は、計算式から明らかなように帰還量に応じて負荷の値が変化します。（帰還量が多くなるほどV1はより大きく、V2はより小さくなります。）

どうしてなのでしょうか？　よくわかりません。

「KAKUSAN真空管アンプ」へ戻る　　　「片側入力の差動回路の解析」へ戻る