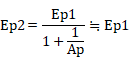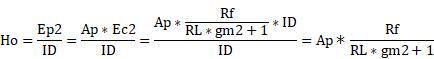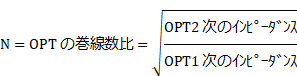|
���R�Ɋǐڑ�(Ver.1) 50BM8 �V���O���E�A���v ����4���@�@�������� |
Ver.02 2019/06/20
|
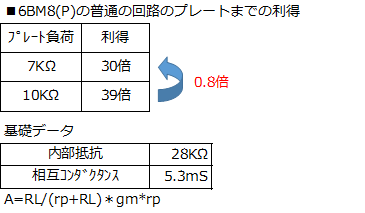
�o�͊�V2�̃v���[�g���ׁi�o�̓g�����X��1���C���s�[�_���X�j��7K���Ƃ����Ƃ��̑��������́A������10.5�{�ƂȂ�܂����B10K�����ׂ̂Ƃ��͎�����8.9�{�ł����̂ŁA10K������7K���ɂ������Ƃ�����������1.2�{�ɑ������܂����B ����A�o�̓g�����X�̃C���s�[�_���X��ɂ�錸�����́A2���C���s�[�_���X��8���Ƃ���ƁA1���C���s�[�_���X��10K���̂Ƃ���0.028�{�A7K���̂Ƃ��̂�0.034�{�ɂȂ�܂�����A�o�̓g�����X�P�̂ł̗�����́A7K���ł�10K���Ƃ���1.2�{�ƂȂ�͂��ł��B �Ƃ������Ƃ́A�o�͊�V2�̃v���[�g���ׂ�10K������7K���ɂȂ����ɂ�������炸�A�o�͊�V2�̃v���[�g�܂ł̗����́A�قڕω����Ă��Ȃ��A���ƂɂȂ�܂��B 6BM8(P)�̕��ʂ̑�����H�Ȃ�A�v���[�g���ׂ�10K������7K���ɂ���ƁA�v���[�g�܂ł̗����́A���݃R���_�N�^���X�Ɠ�����R����T�Z�������0.8�{�ɗ����܂��B �ǂ��䂤���Ƃł��傤���H�@ �����̏�ł́A���A�҂ɂ���p�Ƒz��ł��܂����A���������ڂ����m�肽���āA��H���g���[�X���܂����B �܂��A�����[�����Ƃ�������܂����̂ŁA�܂Ƃ߂Ă����܂��B |
|
|
|
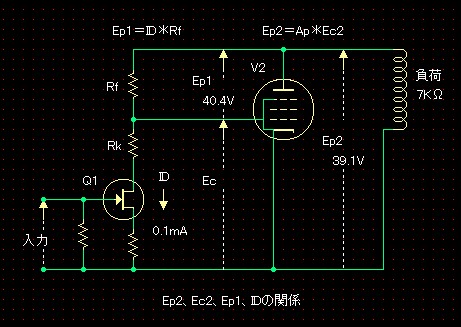
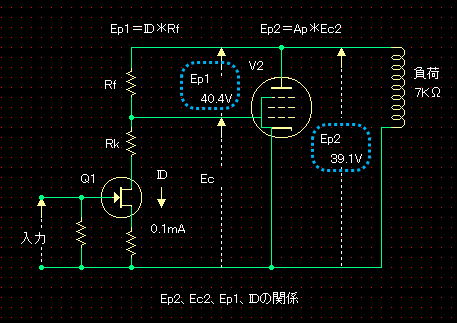
��@��H���g���[�X �E�}�Ńg���[�X���������v�Z���Ă݂܂��B �A�Ҋ�V1�̃v���[�g�|�J�\�[�h�ԓd��Ep1�́A�o�͊�V2�̃v���[�g�d��Ep2�ƃo�C�A�XEc2�ŕ\���ƁA Ep1=Ep2�|Ec �܂��A�o�͊�V2�̃O���b�h����v���[�g�܂ł̑�������Ap�Ƃ���� Ep2���|Ec*Ap �]���āA Ep2��Ep1/(1+1/Ap)�@�E�E�E�@�@ �ƂȂ�܂� �@������A������Ap���傫����AEp2��Ep1�Ƃقړ����l�ɂȂ�AV2�̕��ׂɈˑ����Ȃ��Ƃ������Ƃ�������܂��B
|
|
|
���ɁA���i��H�̑��݃R���_�N�^���X��1mS�������Ƃ���ƁA�}100mV�̐M�������͂��ꂽ�Ƃ��A�h���C���d���i���i���^��ǂȂ�v���[�g�d���j�̕ω��ʂ́}0.1mA�ł��B�A�Ҋ�V1�̐^��ǒ�R�l��404K���������̂ŁA���́}0.1mA�̓d���ω��ɂ��A�Ҋ�V1�̃v���[�g�|�J�\�[�h�Ԃɂ́A�}40.4V���}0.1mA*404K���̐M���d��������܂��B�i��}��Ep1�ł��B�j �����ŁA�o�͊�V2�E6BM8(P)�̃O���b�h����v���[�g�܂ł̑�����Ap�́A�v���[�g���ׂ�10K���̂Ƃ��͖�39�{�A�܂��A7K���̂Ƃ���30�{�ł��̂ŁA�iV2��gm=5.3mS�Arp=28K�����v�Z�j �o�͊�V2�̃v���[�g�Ɍ����M���d��Ep2�́A�@������A �v���[�g���ׂ�10K���̂Ƃ��AEp2��Ep1/(1+1/Ap)��40.4V/(1+1/39)��39.4V �v���[�g���ׂ�7K���̂Ƃ��AEp2��Ep1/(1+1/Ap)��40.4V/(1+1/30)��39.1V �ƂȂ�܂��B �ȏォ��A�o�͊�V2�̃v���[�g�܂ł̗������A�v���[�g���ׂ�7K���̂Ƃ��͕���10K���̂Ƃ��Ɣ�ׁA0.99�{=39.4V/39.1V�ƂȂ�A�قƂ�Ǖω����܂����B
��H�\���I�ɂ́A�A�Ҋ�V1�̃v���[�g�i�ƃJ�\�[�h�ԁj�Ɍ����M�����o�͊�V2�̃v���[�g�d���ƃo�C�A�X�ɉ��~�悭���z������A�Ƃ������Ƃł��傤���B
|
|
|
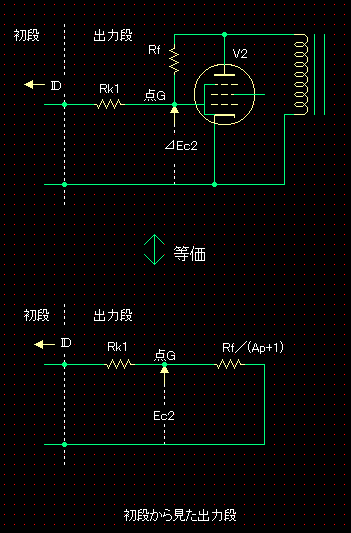
��@�o�͒i�̓d���E�d���ϊ����� ��ɏ��i����̐M���d�����ǂ��o�͊�V2�̃v���[�g�d���ɂȂ�̂����g���[�X���܂����B�����ł́A����ɁA������H�ŏo�͒i�̓d���E�d���ϊ����������߂Ă݂܂��B �A�Ҋ�V1��^��ǒ�R�Ƃ��Ă݂��Ƃ��̒�R�l��Rf�A�o�͊�V2�̑��݃R���_�N�^���X��gm2�Ƃ����Ƃ��A���i�̕���RL1�́A���L�ŕ\�����Ƃ��ł��܂����B�i�u���[�h���C���������Ă݂��v���Q�Ɓj ���i�̕���RL1��Rk1�{Rf/(RL*gm2+1)�@ �E�}����A���i�̕���RL1���g���āA�o�͒i�ɐM���d��ID�����ꂽ�Ƃ��A�o�͊�V2�̃O���b�h�ւ̓��͐M��Ec2�����߂�ƁA
�Ȃ̂ŁA �o�͒i��d��/�d���ϊ���H�Ƃ݂��Ƃ��̗���Ho�́A�o�͊�V2�̓�����R��rp2�Ƃ����
����āA
�ƂȂ�܂��B |
|
|
² �o�͒i��d��/�d���ϊ���H�Ƃ݂��Ƃ��̗����́A�A�Ҋ�V1�̒�R�l�ŋߎ�����邱�Ƃ�������܂����B�܂��A�A���v�̗������҂�������ARf��傫������Ηǂ����ƂɂȂ�܂��BRf=rp1+��1*Rk1�Ȃ̂ŁA�������̑傫��3�ɊǂقǗ����ʂł͗L���ł��B ² �o�͒i�̗�������A�o�͊�V2�̃p�����[�^�������Ă��܂��܂����B�@�g�[��P-G�A�ҁh �̂Ȃ���Ƃ��Ǝv���܂��B �@ |
|
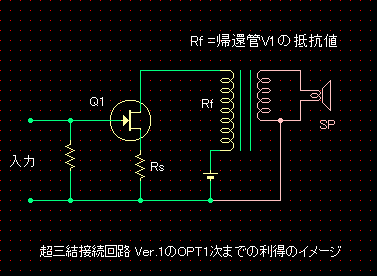
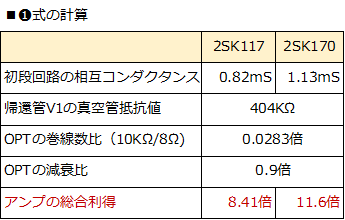
��@��H�S�̂̑�������A ��H�S�̂̑�������A�́A���i��d��/�d���ϊ��A�o�͒i��d��/�d���ϊ��Ƒ�����ƁA��̌��ʂ���A�ȉ��̂悤�ɂȂ�܂����B
�����ŁAgm1�����i��H�̑��݃R���_�N�^���X�ARf���A�Ҋ�V1�̒�R�l Dt��OPT��1������2���ւ̓d�͑����i0.8�`0.9�ʂ������ł��j
|
�@ |
|
��@❶���͂ǂ̂��炢�̋ߎ��H ❶���́A�ߎ����ł��B������H�œ����o���Ă��܂��ƁA�ǂ̂��炢�̋ߎ��Ȃ̂����ϓI�ɔc�����ɂ����̂ł����A��Ɏg�����}������Ɩ��炩�ŁA�o�͊�V2�̃v���[�g�Ɍ����M���d��(Ep2)�́A�A�Ҋ�V1�iRf�j�̃v���[�g�Ɍ����d���iEp1�j�ɓ������Ƃ��Ă��܂��B ��������Č���ƁA������Ƌߎ��Ƃ������T�Z�ł��ˁB
|
|
|
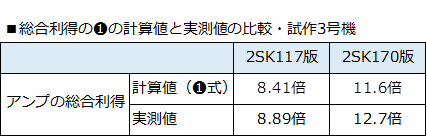
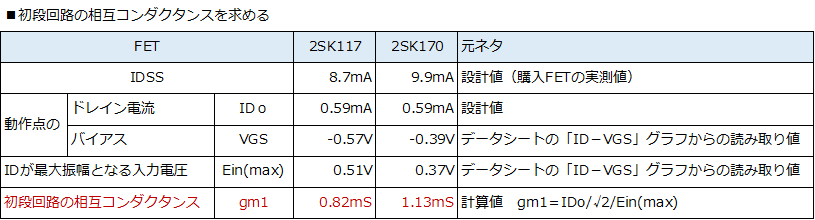
����3���@�̎����l��❶���ɂ��v�Z�l�Ƃ��r���Ă݂܂��B ❶���ł́A���i��H�̑��݃R���_�N�^���X�̒l���K�v�ł��B���̑��݃R���_�N�^���X�̒l�́A�u����3���@�@��ւ�FET�̑I���v�ŋ��߂��A�h���C���d���̍ő�U���̒l�Ƃ��̓��͓d���̃f�[�^������܂��̂ŁA����炩�狁�߂邱�Ƃɂ��܂����B ���\����r���ʂł��B���̐��藧�����班�Ȃ߂Ɍv�Z����܂����A❶���́A�v���̊T�Z�Ƃ��Ă͂��������ł��傤���B
�@ |
|
�@