|
���R�Ɋǐڑ�(Ver.1) 50BM8 �V���O���E�A���v ���[�h���C���������Ă݂� |
Ver.01 2015/12/7
|
����3���@���������A�������̋L���̒ǎ��͂���ł����܂��ł��B�ǎ��́Y�Ƃ��āA����{�Ƃ������O��Ver.1�̉�H�́A�o�͊�V2�A�A�Ҋ�V1�A���i�̃��[�h���C���������Ă݂܂����B
|
|
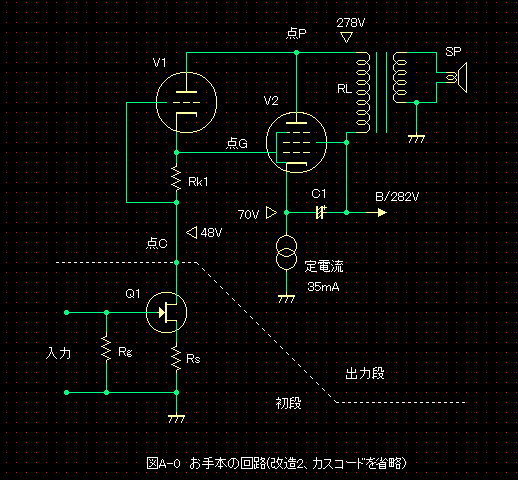
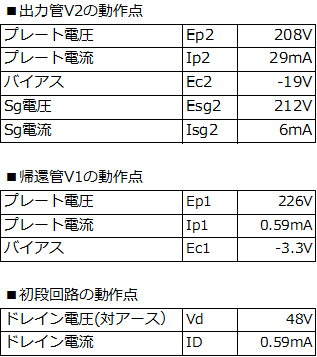
��@��H��V1��V2�̓���_ �g���[�X������H�́A���L�̉�H�ł��B���i��FET�Ƃ�������3���@�i����{�̉���2�j���x�[�X�ɂ������i�̃J�X�R�[�h��H�͏ȗ����Ă��܂��B���̉�H�ł̓���_�ł����A����{�̋L���ɂ́A����_���L�ڂ���Ă��܂���B�����ŁA�L���ɋL�ڂ���Ă���d���l�����ɃV�~�����[�V�������A����_�����߂܂����BSG�d���������@�Ǝ��������܂����C�ɂ��Ȃ����Ƃɂ��܂��B |
|
�@�@ |
|
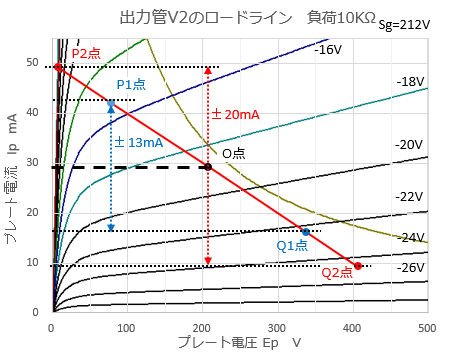
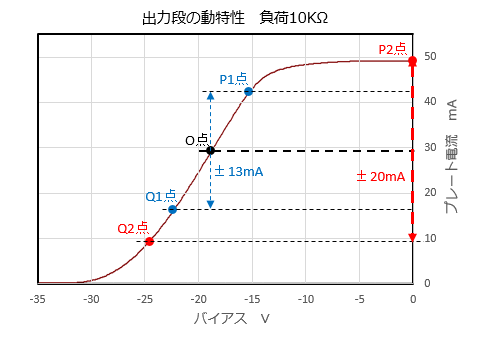
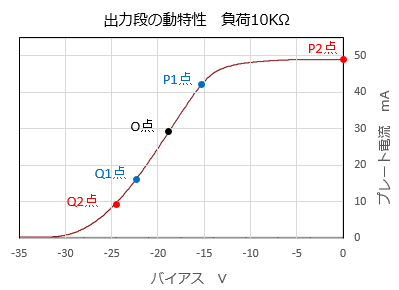
��@�o�͊�V2�̃��[�h���C�� ���̂悤�ȏ����Ń��[�h���C���������Ă݂܂����B ² ���O���ڑ���H�́A�[��P-G�A�҂ɂ��o�͐M���̘c�݂����Ȃ��Ȃ��H���Ǝv���܂��B�i����@�̗�ł͍ő�o�͂�2%���x�j�B���̂��Ƃ���A���[�h���C���������_�𒆐S�Ƃ������̐U���ʂƕ��̐U���ʂ͓������A�Ƃ��܂��B ² �o�͐M����OPT��1�����Ə��i���ɗ���܂����A���i���ɗ����o�͐M���́AOPT��1�����ɔ�r���ĂƂĂ����������߁A�o�͊�V2�̕����́AOPT��1�����C���s�[�_���X��10K���A�Ƃ��܂��B ² P-G�A�҂̓O���b�h�d���������̈�͋��Ȃ̂ŁA�ő�o�͓_�̃o�C�A�X��0V�ȉ��A�Ƃ��܂��B
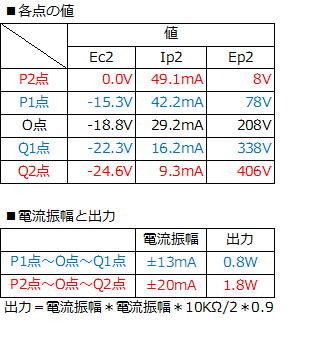
���}���A���̏������ň����Ă݂��ő�o�͂̂Ƃ��̃��[�h���C���i�_P2�`����_O�`�_Q2�j�ł��B�o�C�A�X���|10V�ȉ��̗̈�́A�eEP-IP�����Ȑ����d�Ȃ��Ă���A�o�C�A�X�̒l�������ɂ��Ă��卷�������ł����A�����́A���E��0V�܂ŁA�Ƃ��Ă���܂��B���̂Ƃ��̃v���[�g�d���̐U���́}20mA�ŁA�T�Z���o�͂�1.8W�i��20mA*20mA*10K��/2000*0.9�j�ƂȂ�܂����B �܂��A�o�C�A�X�̕ω��́A�OV�`�|18.8V�`�|24.6V�ƂȂ��Ă��āA���͐M���i�O���b�h�|�J�\�[�h�ԓd���j�̐U���́A�{18.8V�`0V�`�|5.8V�ł��B�c�̖������i�̏o�͓d���i���o�͒i�̓��͓d���j�Ƀv���[�g����̑��ʂ̋A�ғd�������Z����āA���̂悤�ɔ��ɃA���o�����X�ȓ��͐M�������������͂��A�Ƃ̑z��ł��B �_�iP1�AQ1�j�́A�������̗ǂ������ł��B�U���́}13mA�ŁA�o�͂͊T�Z��0.8W�A���̂Ƃ��̏o�͊�V2�̓��͐M���́A�����Ńo�����X�̗ǂ��i�c�݂̏��Ȃ��j�{3.54V�`0V�`�|3.59V�ł��B |
|
�@ |
|
�g�_�iP1�AQ1�j�͒������̗ǂ��h�A�ƌ����Ă����[�h���C���ł͎��o�I�ɂ͕������ł����A�������}�Ō���Ɨǂ�������܂��B�撣���ăo�C�A�X���OV�ɂȂ�܂ŐU���Ă��A�v���[�g�d���̑������݂��Ȃ��ďo�͂��オ�肻���ɂ���܂���ˁB
|
|
�@☞�@�ƂĂ��ȈՂȂ����ŏo�͊�V2�̃��[�h���C���������܂����B�ȈՂȂ��ɂ́A������̂ł͂Ȃ����Ǝv���܂��B
|
|
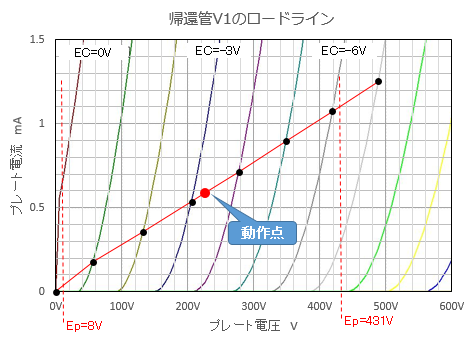
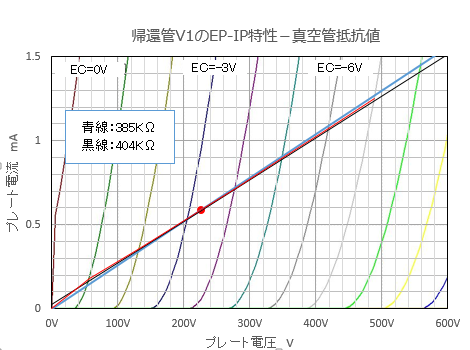
��@�A�Ҋ�V1�̃��[�h���C�� �㞊����́w��3�Ɋǐڑ��u�����D1�̓����}��`���Ă݂悤�̃R�[�i�[�x�̉���ɉ����āA�o�C�A�X�l�i0V����|7V�܂Łj�ƃJ�\�[�h��RRk1�i5.6K���j����A�v���[�g�d��Ip1�����߂āA6BM8(T)��EP-IP�����}��Ƀv���b�g���āA�e�_�����т܂����B
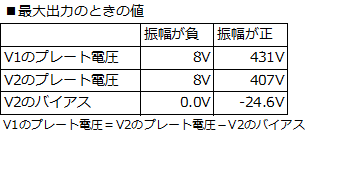
����_�́AEp=226V�A�o�C�A�X=-3.3V�AIp=0.59mA�ł��B �g V1�̃v���[�g�d����V2�̃v���[�g�d���|V2�̃o�C�A�X �h �̊W�����藧���܂��̂ŁA��ɋ��߂�V2�̃v���[�g�d���ƃo�C�A�X�l����A�ő�o�͂̂Ƃ���V1�̃v���[�g�d���̐U���́A8V�`226V�`413V�ł��B�@8V�Ƃ����Ԃ�ƒႢ�d���܂Ŋ��p���Ă���Ȃ��A�Ƃ�����ۂł��B�܂��A�A�Ҋ�V1�̕����́A������^��ǒ�R�ƌĂ���H�ŁA�g�O����݂�ƂقƂ�ǒ�R��Ƃ݂Ȃ���h�g �A�Ƃ������Ƃ����̃��[�h���C���ŗǂ�������܂����B |
|
�@�@ |
|
���ɁA�����A�Ҋ�V1���R��ƌ��Ȃ����Ƃ��̒�R�l�i���[�h���C���̌X���̋t���j���v�Z���Ă݂܂��B ���@�́A2�������āA ���@�@ �A�Ҋǂ̕�����^��ǒ�R�Ƃ���3�萔����v�Z����ƁA404K���ƂȂ�܂��B Rf=rp1+��1*Rk1��404K�� ���@�A ���[�h���C�����A����_�i226V�A0.587mA�j�ƌ��_�i0V�A0mA�j��ʂ钼���ƌ��Ȃ��ƁA385K���ƂȂ�܂��B Rf��Ep1/Ip1��385K�� |
|
|
���}�́A��Ɉ��������[�h���C����1/404K���A1/385K���̌X���̒��������ꂼ����d�˂��}�ł��B3�{�Ƃ��d�Ȃ��Ă���卷�͖����ł��B�i����́A�������̗ǂ�������I��ł��邩�����Ǝv���܂��j
�@ |
|
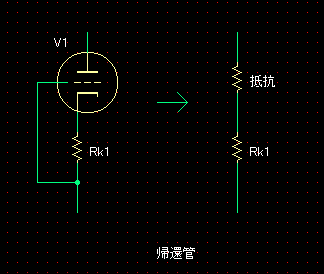
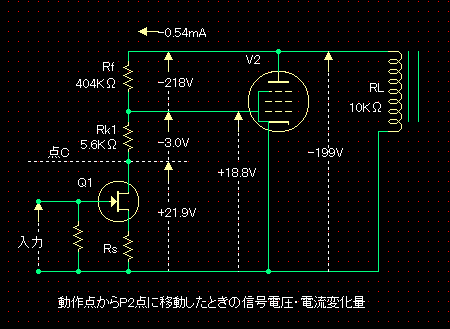
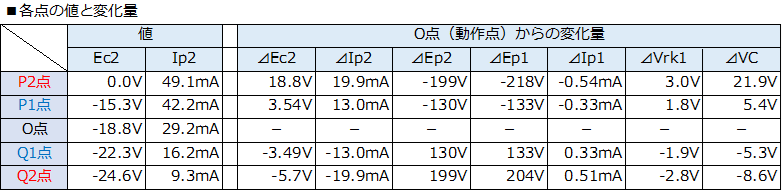
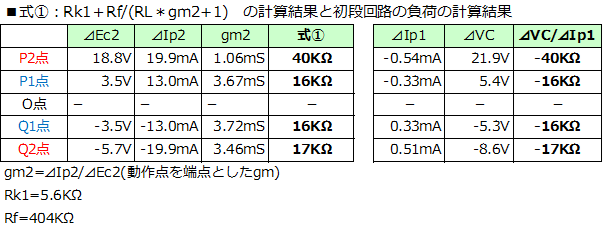
��@���i��H�̓��� �E�}�́A�A�Ҋ�V1��404K���̒�R�ɒu��������������H�ł��B ���A�M�������͂���āA�o�͊�V2������_��O�_����ő�o�͓_��P2�_�Ɉړ������Ƃ��܂��B ���̂Ƃ��́A��H��̊e���ʂ̓d���A�d�����ω������g���[�X����ƁA �܂��A�o�͊�V2�̃o�C�A�X�̕ω��ʇ�Ec2�ƃv���[�g�d���̕ω��ʇ�Ep2�́AO�_��P2�_�̃o�C�A�X�ƃv���[�g�d�����A���ꂼ��A-18.8V��208V�A�OV�ƂWV�������̂ŁA�i���[�h���C������ǂݎ�����l�j �E��Ec2�FV2�̃o�C�A�X�́A18.8V���� �E��Ep2�FV2�̃v���[�g�d���́A199V����
|
|
|
���̂��Ƃ���A
�����͂��ł��B �]���āA�M�������͂���āA�o�͊�V2��O�_����P2�_�Ɉړ������Ƃ��A���i�̓���́A�h���C���d����0.54mA�������A�h���C���d���i�A�[�X�j��21.9V���������͂��ł��B
���l�ɁA�c���P1�_�AQ1�_�AQ2�_�ɂ��āA�ω��ʂ��g���[�X���A���ʂ����\�ɐ������܂����B
|
|
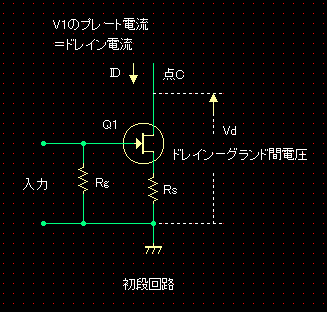
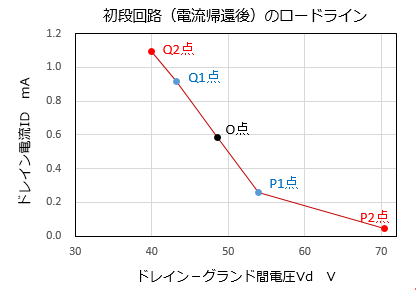
♬�@���i��H�S�̂̃��[�h���C�� �d���A�҂��{���ꂽ���i��H���I�ɂЂƂ�FET�ƌ����Ă��Ƃ��A����FET�� ² �h���C���d��ID��V1�̃v���[�g�d��Ip1 ² �h���C���d��Vd��C�_�̓d���i�A�[�X�j �ł��B ����_�ł́i���͐M���������Ƃ��́jID��Vd�́A0.59mA��49V�������̂ŁA��L�\����A�e�_��Vd��ID���v���b�g�����[�h���C���������Ă݂�ƁA���}�̂悤�ɂȂ�܂����B �ʔ������ƂɁA�����ł͂���܂���I�I�@P1�_����X�����Q��P2�_�Ɏ���܂��B
���ӁGQ1�P�̂̃��[�h���C���ł͂Ȃ��A���i��H�S�̂̃��[�h���C���ł��B �@ |
|
��@���i��H�S�̂̃��[�h���C���̌X�� ���i�ʔ������ƂɁA���i��H�̃��[�h���C���́A�Ȑ��ł����B���́A�Ȑ��ɂȂ�̂ł��傤���H�@���̋Ȑ��̐��̂́A���҂ł��傤���H
���[�h���C���̌X���́A�h���C���d���̕ω��ʇ�ID�^�h���C���d���i�O�����h�j��Vd �Ȃ̂ŁA���̋t���́A���i��H�̕��ׁi����Vd/��Ip1�j�ł��B�����āA���i��H�̕��ׂ́A�o�͒i�̓��̓C���s�[�_���X���̂��̂ł��B�i�������A�d���̗������������Ȃ̂ŁA�������t�ɂȂ�܂��B�j �Ȃ̂ŁA���i��H�̃��[�h���C�����Ȑ��Ƃ������Ƃ́A���O�Ɋǐڑ���H�̏o�͒i�̓��̓C���s�[�_���X�͈��ł͖����A�Ƃ������Ƃ������Ă��܂��B �z���g�ł��傤���H
|
|
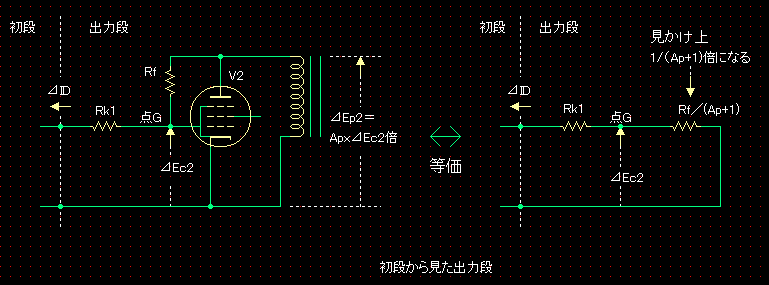
���}�i�E���j�́A���i��H���猩���o�͒i�̉�H�ł��B�i�A�Ҋ�V1���RRf�ɒu�������Ă��܂��B�j�@ �ǂ�����ƁA�P����P-G�A�҂̉�H�ł��B���̉�H�̓��̓C���s�[�_���X�́A�ȉ��̂悤�ɂȂ�܂��B�i�ڂ����́A�uP-G �A�҉�H�̓��̓C���s�[�_���X�v�����Q�Ɖ������B�j
�o�͒i�̉�H�̓��̓C���s�[�_���X�́A�o�͊�V2�̑��݃R���_�N�^���X��gm2�Ƃ���AV2�̕���RL�ɑ���V2�̓�����Rrp2���\���ɑ傫���A�܂��A�A�Ғ�RRf��V2�̕���RL�ɑ��ď\���傫����AAp2��gm2��RL�ł�����A
�ƂȂ�܂��B �@������A�o�͒i�̉�H�̓��̓C���s�[�_���X�́A���݃R���_�N�^�Xgm2�̋t���Ɉˑ����邱�Ƃ�������܂����B�o�͊�V2�̑��݃R���_�N�^���Xgm2�́A���[�h���C����̈ʒu�ɂ�肻�̒l�͕ω����܂��B�]���āA�@���������O�Ɋǐڑ���H�̏o�͒i�̓��̓C���s�[�_���X�͈��ɂ͂Ȃ�Ȃ��A�Ɨ������܂����B
�@�������Z���Ă݂܂��B�\�̍����͇@�����狁�߂��l�A�\�̉E���͐�ɋ��߂��h���C���d���ƃh���C���d������v�Z�����l�ł��iO�_���N�_�Ƃ����l�ł��j�B�ǂ���v���Ă��܂��B
�Ō�ɁA�{���̔��[�́A���̂Q�̓��������āA�������Ă���Ȃ��A�Ǝv�������Ƃł��B�������Ȑ��̌X���̋t���́A1/�iRL*gm2�j�ɋߎ�����܂��B�Ȑ��̋Ȃ����͎��Ă���͂��ł����B |
|
|
|
|
|
|
|
��@���i��H�ɘc�݂������Ƃ����� ����_����P2�_�̃h���C���d���̕ω��ʂ́|0.54mA�AQ2�_�ł�0.51mA�ƂȂ�܂����B���i��H�ɘc�݂������Ƃ���A���͐M���Ɩ����������܂��B ����́AV2�̃��[�h���C�����Ђ����Ƃ��̏����w���O���ڑ���H�́A�[��P-G�A�҂ɂ��o�͐M���̘c�݂��ƂĂ��Ⴍ�Ȃ�܂��B���̂��Ƃ���A���[�h���C���̐U�镑���́A����_�𒆐S�Ƃ������̐U���ʂƕ��̐U���ʂ͓������A�Ƃ��܂��B�x�ɋN�����Ă��邩�ƍl�����܂��B ���ɁA���i��H�S�̂̑��݃R���_�N�^���X��0.54mS�Řc�݂�������A���͐M�����}1V�̂Ƃ��̃h���C���d���̐U���́}0.54mA�ł�����AP2�_�͂��̂܂܂ŁAQ2�_�̃h���C���d���́A1.09mA��葽���Ȃ��āAQ2�_��V2�̃��[�h���C����ł͂��������E���Ɉړ�����̂ł͂Ȃ��ł��傤���H�i�A�Ҋ�V1�ɘc�݂�������j �܂��A���i��H�̏o�͓d���ɘc�݂������āA���͐M�����}1V�̂Ƃ��̃h���C���d���̐U�����|0.54mA�`0.51mA�ŁA�i�A�Ҋ�V1�ɘc�݂�������j�A�X�s�[�J�[�q�ɂ͘c�݂̖����M�����o�͂����A�Ƃ������Ƃ��Ǝv���܂��B �@ |
�@