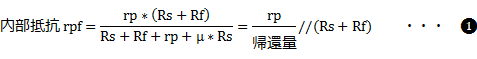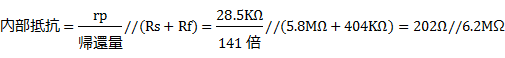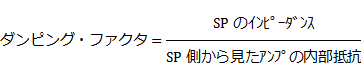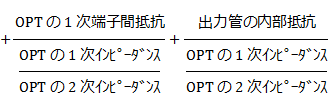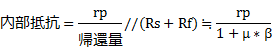|
���R�Ɋǐڑ�(Ver.1) 50BM8 �V���O���E�A���v ������R�ƃ_���s���O�E�t�@�N�^ |
Ver.01 2015/12/7
|
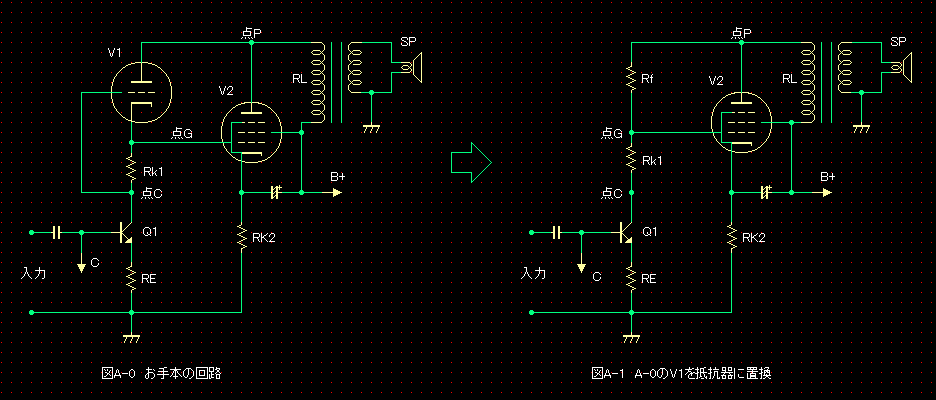
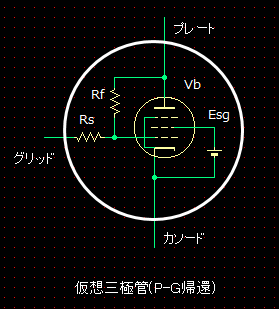
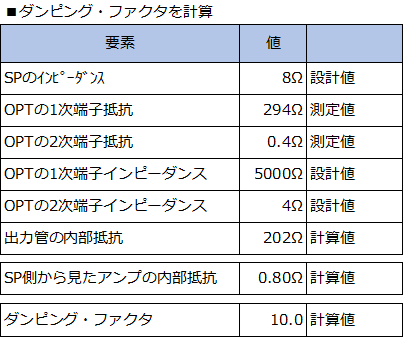
����1���@�̓����Ŗڂ�������̂��A�_���s���O�E�t�@�N�^�̍����ł��B������10�ł����B �_���s���O�E�t�@�N�^�������Ƃ������Ƃ́A�o�͊ǂ̓�����R���Ⴂ�Ƃ������Ƃł��B����̐���ŁA���낢��������Ă�������u���O�Ɋǐڑ��̍l�����Ɛv�w�j�v�ɂ��A�u���O�Ɋǐڑ���H�v�́A�[��PG�A�҂ɂ���ĒႢ������R�Ă��������ł��B �}A-0�́A����{�Ƃ����u��3�Ɋǐڑ�Ver.1 6BM8 �V���O�� �X�e���I�p���[�A���v �U�v�̑�����H�ł��B ���̑�����H�̒��ŁA�_P����_C�܂ł̊Ԃ̉�H�́A�u�^��ǒ�R�v�ƌĂ���H�ŁA�O������݂���قƂ��1�{�̒�R��Ɠ����A�������ł��B�����ŁA���̎O�Ɋ�V1���R��Rf�ɒu����������H���A�}A-1�ł��B�������ĎO�Ɋ�V1���R��ɒu����������H�}�ɕϊ����Ă݂�ƁA�Ȃ�ق�P-G�A�҂ł��邱�Ƃ��ǂ��킩��܂��B�i�O�Ɋ�V1���u�A�Ҋǁv�ƌĂԂ����ł����A�������Ė����Ǝv���܂��B�j
P-G�A�҂Ƃ������_�ŁA����{�Ƃ����u���O�Ɋǐڑ���H�v�̏o�͊ǂ̓�����R���v�Z���Ă݂܂��B�������������ɂȂ��Ă���̂ł��傤���H |
|
�@�@ |
|
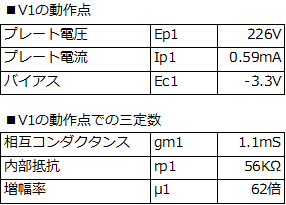
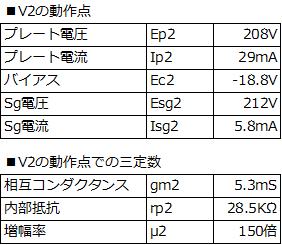
��@V1�AV2�̓���_�ł̎O�萔 ������R���v�Z���鏀���Ƃ��āAV1�AV2�̓���_�ł̎O�萔�����߂Ă����܂��B����{�̋L���ɂ́AV1�AV2�̓���_�́A���m�ɋL�ڂ���Ă��܂���̂ŁA����{�̉�H�}�ɋL�ڂ��ꂽ�d���l���V�~�����[�^��H�ɐݒ肵�āAV1��V2�̓���_���߁A�����ŁA���̓���_�ł̎O�萔�܂����B
|
|
|
|
|
|
��@�o�͊�V2�̓�����R�̓����� |
|
|
�܋Ɋǂ�P-G�A�҂��{������H���ЂƂ̐^��ǁi���z�I�ȎO�Ɋǁj�ƌ��Ȃ����Ƃ��A���̓����́A�O�ɊǓI�ȓ����ƂȂ�A������R�́A���̂悤�ɂȂ�܂��B
������
☞�@���̕ӂ�́A����P-G�A�҂Ɋւ�����Ȃ��l�@�u4.1�@���z�O�Ɋǂ̎O�萔�v �����Q�Ɖ������B �@ |
|
|
����❶�����疾�炩�Ȃ悤�ɁAP-G�A�Ҍ�̓�����R�́A�A�Ғ�RRf�ARs�̒l��������A�v�Z�ł���Ƃ������ƂɂȂ�܂��B�ȉ��A���ɁA����{�Ƃ����u���O�Ɋǐڑ���H�v�̋A�Ғ�RRf�ARs�̒l�����߂Ă����܂��B |
|
|
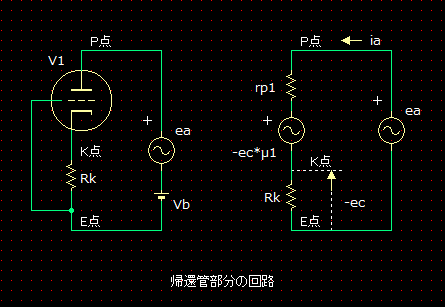
♬�@�A�Ғ�RRf�̒l �A�Ғ�RRf�́A�A�Ҋ�V1���R��ƌ��Ȃ����Ƃ��̒�R�l�ł��B�E�}�́A�A�Ҋ�V1�����̉�H�̓�����H�ł��B���̓�����H���g���āARf�����߂Ă݂܂��B P�_��E�_�Ɍ𗬓d��ea��^�����Ƃ��ɁA�����𗬓d����ia�ARk1�̒[�q�ԂɌ����𗬓d�����|ec�A�A�Ҋ�V1�̑���������1�A������R��rp1�Ƃ���ƁA������H����A���̂Q�������藧���Ƃ�������܂��B
����2������A�_P����_G�̊Ԃ̒�R�l��Rf�Ƃ���ƁARf�́A
�ƂȂ�܂��B
❷���ɁAV1�̎O�萔�̒l��Rk1�̒l��������ƁARf�̒�R�l��404K���ƂȂ�܂����B
|
|
|
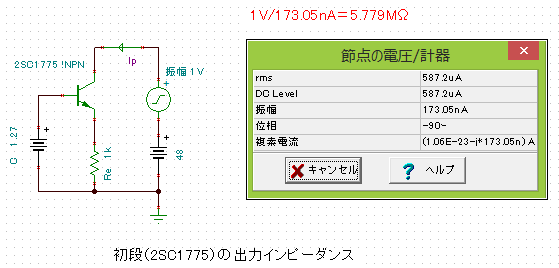
♬�@�A�Ғ�RRs�̒l �A�Ғ�RRs�̒l�́A�A�Ҋ�V1�̃J�\�[�h��RRk1�Ə��i�̏o�̓C���s�[�_���X�����Z�����l�ł��B ����{��H�̏��i�́A�g�����W�X�^�[�̓d���A�҉�H�ł��B�g�����W�X�^�[�̐U�镑���́A���s���ŁA�G�~�b�^��RRe���^����ꂽ�G�~�b�^���ʁi�R�����j��H�̏o�̓C���s�[�_���X���A�ǂ̂悤�Ɍv�Z����悢�̂�������܂���B �����ň�����Tina�ŃV�~�����[�V�������Ă݂��Ƃ���A5.8M���ƂȂ�܂����B�i2SC1775A�̃f�o�C�X���f���́A�K�i�\����K���ɍ��܂����B�j �J�\�[�h��RRk1�́A�o�̓C���s�[�_���X5.8M���ɔ�ׁA�����ł���قǏ������̂ŁARs�̒l�́A5.8M���ƂȂ�܂����B Rs=���i�̏o�̓C���s�[�_���X+�A�Ҋ�V1�̃J�\�[�h��RRk1��5.8M���@ �@ |
|
�@�@�@ |
|
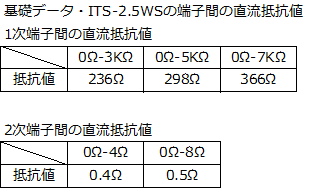
��@�o�͒i�̓�����R���v�Z ����Ō��l�^���������̂ŁA❶������AP-G�A�҂��{�����o�͊�V2�̓�����R�̒l���v�Z����ƁA202���ƂȂ�܂����B
���ʂ̕��A�ҁiP-G�A�ҁj�̂����ŁA28.5K��������6BM8(P)�̓�����R���A��������202���ɂ܂Œቺ���Ă��܂����B �@ ♬�@�A�җ� Rs�̒�R�l5.8M���́ARf�̒�R�l400K���Ɣ�ׂ�10�{�ȏ�ƂȂ�ƂĂ��傫�Ȓl�ł��B�A�җʃ���Rs/(Rs+Rf)�́A0.9�ȏ��ɂȂ�܂����B�g�[��P-G�A�ҁh�ƌ����邾���̂��Ƃ͂���܂��B �@ |
|
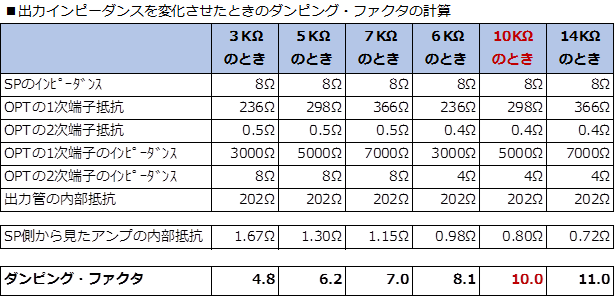
��@�_���s���O�E�t�@�N�^���v�Z OPT(ITS-2.5WS)�̒[�q�Ԃ̒�R�l���������A�o�͊�V2�̓�����R�l��202�������ɁA����1���@�̃_���s���O�E�t�@�N�^���v�Z�����Ƃ���A10.0�ƂȂ�܂����B �����l10�Ɨǂ������Ă��܂��B
|
||
|
���FOPT��2���[�q�Ԓ�R�̒l0.4���́A�L�����������_��1�ʂ܂ł�DMM�ő��肵���l�ŁA�ڐG��R��덷�����鐔�l�ł��B����0.5���Ȃ�_���s���O�E�t�@�N�^�͂X�A�܂��A0.3���Ȃ�12�ƌv�Z����܂��B |
�@ |
|
|
Note1 �V�~�����[�V�����ŋ��߂����i�̏o�̓C���s�[�_���X��5.8M���ł������A��������2SC1775A�̃f�o�C�X���f�������܂ЂƂ������悤�ŁA���@�́A8M���`�XM�����炢�͂���悤�ł��B9M���œ�����R�l�ƃ_���s���O�E�t�@�N�^���Čv�Z�����197����10.1�ƂȂ�܂����B�����܂ő傫���ƁA5.8M���ł�9M���ł�������R�l�ɍ��͏o�܂����ˁB |
|
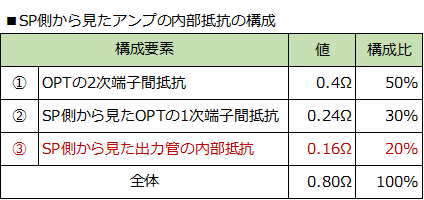
Note2 SP�����猩���A���v�̓�����R�́A0.8���ł����B����0.8�����\������v�f�́A�@ OPT��2���[�q�Ԓ�R�A�A SP�����猩��OPT��1���[�q�Ԓ�R�A�B SP�����猩���o�͊ǂ̓�����R��3�P�ł��B ����̎���1���@�ł̂��ꂼ��̒l������ƁA�B��SP�����猩���o�͊ǂ̓�����R�́ASP�����猩���A���v�̓�����R�S�̂�2���ɂ����܂����B����ł́A�ɂ߂ĒႢ������R�邱�Ƃ��ł��钴�O�Ɋǐڑ���H�̓���������Ă��Ȃ���ۂł��B �[�q�Ԃ̒�����R���ƂĂ��������i�炵���jTAMURA��F-2003������Ńq�A�����O�ł�����Ȃ��A�ȂǂƖϑz���Ă��܂��܂��B �܂��A����y���̒��O�Ɋǐڑ��̍��̂Ȃ��ŁAOPT��2��������I�[�o�I�[���ɕ��A�҂������������������q�����܂����B�I�[�o�I�[���̕��A�҂ł���AOPT�̒[�q�Ԃ̒�R���������㏬�����ł���̂ŁA���̂�������ӎ�����Ă̐��삩������Ȃ��A�ȂǂƎv���܂����B
|
|
Note3 OPT�̒[�q�Ԓ�R���傫�����߁ASP�����猩���o�͊ǂ̓�����R�́ASP�����猩���A���v�S�̂̓�����R��2���ɂ����܂���ł����B 2���ɂ����Ȃ�Ȃ����������߂�ɂ��ẮA❶������v�Z���邽�߂ɂ͓���_��3�萔��A�Ғ�RRs�ARf�̒l���K�v�Ŏ�Ԃ�������܂��B�_���s���O�E�t�@�N�^���T�Z���邾���Ȃ�A�A�җʃ�=1�Ƃ���❶�����ۂ߂� ������R��1/gm �Ōv�Z���Ă��卷�͖������Ǝv���܂��B
���ہA�����̋K�i�\�ɂ���Ep��100V�̓����̐����igm=6.8mS�j�Ōv�Z����ƁA�o�͊ǂ̓�����R��147����1/6.8mS�ŁA202���Ɣ�ׂ�ƍ��ق�����܂����A����147�����g���ċ��߂��_���s���O�E�t�@�N�^��10.6�ƂȂ�A10.0�Ƒ卷�͂���܂���B |
|
Note4 ����A�C�`�J����ITS-2.5WS���A�ꎟ��5K���A2����4���̒[�q�Ŏg�p���A8���̃X�s�[�J�[��ڑ������Ƃ���1�����C���s�[�_���X��10k���ɂȂ�悤�ɂ��Ă��܂��B�C�`�J����ITS-2.5WS�́A�ꎟ����3K���A5K���A7K���̒[�q������܂��̂ŁA���l�̎g�����ŁA6K���A14K���ł̎g�p���\�ł��i��1�j�B�����ŁA1�����C���s�[�_���X���A3K���A5K���A7K���A6K���A10K���A14K���Ƃ����Ƃ��̃_���s���O�E�t�@�N�^���v�Z���Ă݂܂����B �C���s�[�_���X��7K���̂Ƃ��́A�_���s���O�E�t�@�N�^��7.0�ł����B7K�����ǂ������ł��B *1:���̂悤�ȗp�@�́A���܂肨���߂ł��Ȃ������ł��B |
|
|
|