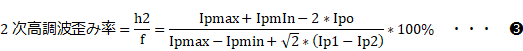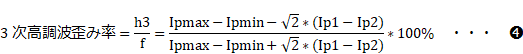|
���[�h���C������Q���c�ݗ��ƂR���c�ݗ����Z�o�ł��闝�R |
2018.5.30
|
SYLVANIA�̃}�j���A���ɁA���[�h���C�����瓾���v���[�g�d���̒l�ɂ���2���̍����g�c�ݗ��Ƒ�3���̍����g�c�ݗ����v�Z������@���L�ڂ��ꂨ��A�������͈͂ł͐��x�ǂ����߂邱�Ƃ��ł��܂����B�@�i�Q�l�@�u���[�h���C������Q���c�ݗ��ƂR���c�ݗ����Z�o�����v�j
�{�e�ł́A�ǂ����ă��[�h���C�������3���̍����g�c�ݗ����v�Z�ł���̂��A���̎d�g�݂��܂Ƃ߂܂��B
|
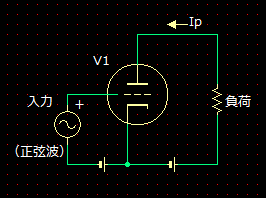
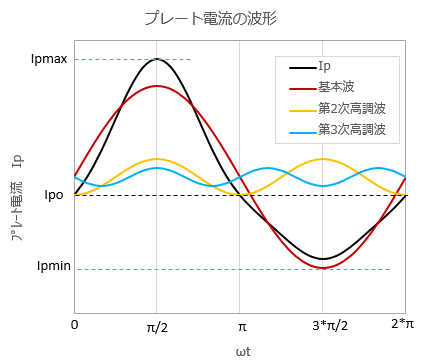
��@�T�v�O���b�h�ɐ����g k*sin(��t) ����͂����Ƃ��A�v���[�g�ɗ����d�� Ip ����{�g�Ƒ�4���܂ł̍����g�ō\������Ă���Ƃ���ƁA���̃v���[�g�d�� Ip �͎��̂悤�ɕ\�����Ƃ��ł��܂��B
������ Ipo�F���M�����̃v���[�g�d�� Ipo+Ipa�F��{�g�A�����g�̒��S�d�� f�F��{�g�̔g���i�ő�U���j hj�F��j�������g�̔g���i�ő�U���j
Ⓐ �̕������̌W���́AIpo+Ipa�A���Ah2�Ah3�Ah4 ��5���ł�����A5�� ��t �̒l�ƑΉ�����v���[�g�d���̒l������A�e�W���̒l�����߂邱�Ƃ��ł��܂��B�i ��ti �� Ipi �Ŋe�W����\�����Ƃ��o����B�j �����g�c�ݗ��́A�g�� f �ɑ���e�g�����l h2�Ah3�Ah4 �̊�����������A����ꂽ�e�W���̒l����e�ՂɌv�Z�ł���A�Ƃ������ƂɂȂ�܂��B �̐S�� 5�̈قȂ� ��t �̒l�ƑΉ�����v���[�g�d���̒l�́A���[�h���C�����瓾���܂��B � ���ɂ� ��t ������݂������Ē��ϓI�ɔc�����ɂ����ł��B�Ⴆ�A�����_�� ��t ��0 �A�ő�v���[�g�d���̂Ƃ��� ��t �� 1/2*���A�܂��A�Ⴆ�A+30V �̓��͂ōő�d���ɂȂ�Ȃ�A������ +15V �̓��͂̂Ƃ��� ��t �� 1/6*���B�i ����Ȃ�ł��傤���ǁA0�x�A90�x�A30�x�̕����܂��܂��ł��B�j |
|
|
♬�@�@�e�W���l�����߂�
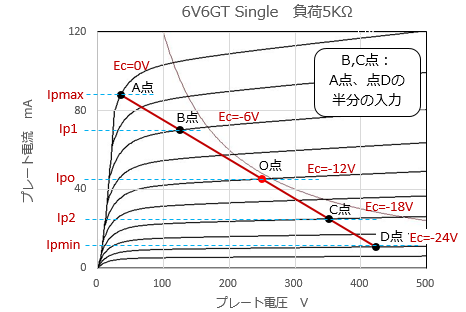
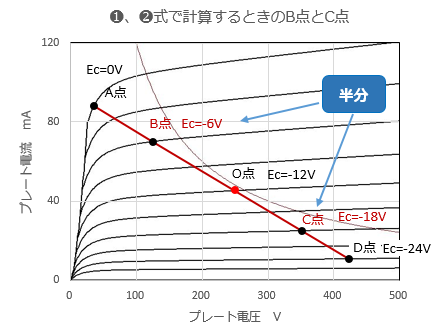
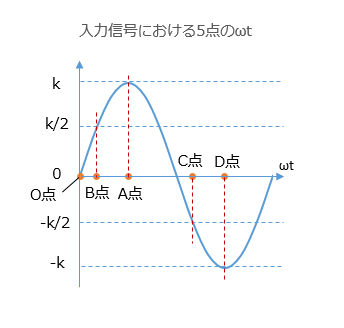
�c����2�_�́A�A���������������₷���悤�Asin(��t)=�}0.5 �ƂȂ�_�Ƃ��܂��BO�_�̃o�C�A�X��0.5�{�A1.5�{�̓_�ł��B�i�o�C�A�X=�OV�܂ŗ�U�����Ƃ��B�j�@����2�_��B�_�AC�_�Ƃ��A���̃v���[�g�d���� Ip1�AIp2 �Ƃ��܂��B �������đI�������e�_�� ��t �̒l��Ⓐ���ɑ������ƁA����5���̘A���������������܂��B A�_�F�ő�v���[�g�d���_�A���̂Ƃ��� ��t �́A��t=1/2*���i90���j
B�_�F���͐M���̐U����A�_�̔����ƂȂ�_�A���̂Ƃ��� ��t �́A��t=1/6*���i30���j
O�_�F�����_�A���̂Ƃ��� ��t �́A��t=0�i0���j
C�_�F���͐M���̐U����D�_�̔����ƂȂ�_�A���̂Ƃ��� ��t �́A��t=7/6*���i210���j
D�_�F�ŏ��v���[�g�d���_�A���̂Ƃ��� ��t �́A��t=3/2*���i270���j
�@���`�D����5���̘A�����������e�W���ɂ��ĉ����āA�v���[�g�d���ŕ\������ƁA
�ƂȂ�܂��B �]���A�ő�v���[�g�d�� Ipmax�A�ŏ��v���[�g�d�� Ipmin�A�����_�̃v���[�g�d�� Ipo �̑��ɁA���͐M�� ein ���ő�l�̔����̂Ƃ��̃v���[�g�d�� Ip1�ƁA�������ŏ��l�̔����̂Ƃ��̃v���[�g�d�� Ip2 �����[�h���C������ǂݎ��A❶���A❷���ɂ��c�ݗ����v�Z���邱�Ƃ��ł��܂��B
�܂��A���σv���[�g�d�� Ipave �́A�����Ōv�Z���邱�Ƃ��ł��܂��B
���A�e�W�������߂鐔���̌o�܂́A�����ɂ���܂��B
|
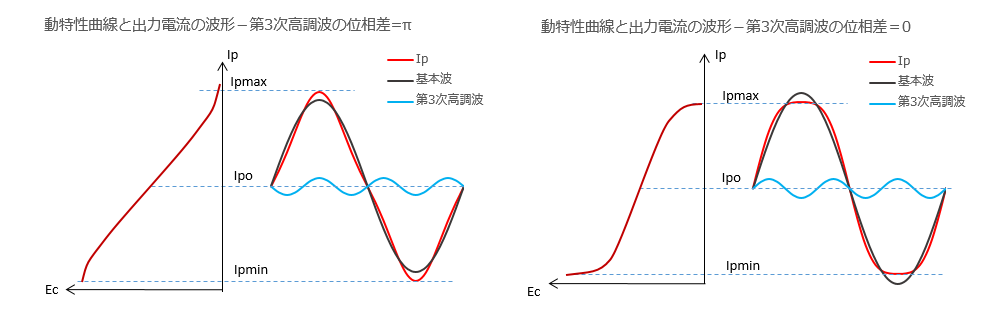
���A��3�������g�̘c���̌v�Z���ʂ��}�C�i�X�ɂȂ�܂������A����́A����6V6GT�V���O���̏o�͐M���̔g�`���A��{�g�ɑ��đ�3�������g�́i��t=0�̂Ƃ��́j�ʑ������[�����������߂��Ǝv���܂��B���}�́A3�������g���܂ޏo�͔g�`�Ƃ��̓������Ȑ��̃C���[�W�ł��B ��{�g�Ƒ�3�������g�̈ʑ������[���̂Ƃ��́A���L�̉E���̓������Ȑ���S�^�ŎR�J���Ԃꂽ�g�`�ɂȂ�A���̂Ƃ��͌v�Z���ʂ��}�C�i�X�ɂȂ�܂��B�iⒶ���͍����̔g�`��z��A3�Ɋǂ�DEPP�Ȃ��ł̔g�`�j
|
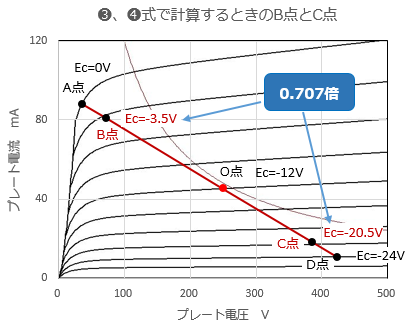
��@�@SYLVANIA�̃}�j���A���ƈႤ�H❶���A❷���́ASYLVANIA�̃}�j���A���ɋL�ڂ���Ă����c�ݗ��̌v�Z���ƈقȂ�܂��B�i�O�́u���[�h���C������Q���c�ݗ��ƂR���c�ݗ����Z�o�����v�Q�Ɓj ����́AB�_�AC�_�̑I�����قȂ邩��ɑ��Ȃ�܂���B ���❶���A❷�������߂��ۂ�B�_�AC�_�́A���͐M�����ő�l�̔����isin(��t)=0.5�j�A�ŏ��l�̔����isin(��t)=-0.5�j�̂Ƃ��̓_�Ƃ��܂������A SYLVANIA�̃}�j���A���ł́A������ǂނƁAB�_�AC�_���A���͐M�����ő�l��1/��2�isin(��t)=1/��2�j�A�ŏ��l��1/��2�isin(��t)=1/��2�j�̂Ƃ��̓_�Ƃ��Ă��܂��B |
|
����SYLVANIA���}�j���A���ɂ����I���������Ƃ��A��Ɠ��l�Ɋe�W�������߂�ƁA
�ƂȂ�܂����B �]���A�c�ݗ����v�Z���鎮�́A
�ƂȂ�A❸���A❹���́ASYLVANIA���}�j���A���ɋL�ڂ���Ă��鎮�Ɠ����ł��B �|�@�e�W�������߂鐔���̌o�܂́A�����ɂ���܂��B
|
|
��@��{�g�Ƒ�2�������g�����ō\������Ă���Ƃ��ȏ�́A�v���[�g�ɗ����d�� Ip ����{�g�����4���܂ł̍����g�ō\������Ă���A�Ƃ��Ă���A��3���܂ł̍����g�����������ɓ_B�Ɠ_C�����߂邱�Ƃ��v������܂��B �v���[�g�ɗ����d�� Ip ����{�g�Ƒ�2���̍����g����\������Ă���A�Ƃ���ƁA�����ƊȈՂɑ�2���̍����g�c���������܂��B
�v���[�g�ɗ����d�� Ip ����{�g�Ƒ�2���̍����g����\������Ă���A�Ƃ���ƁA����Ip��Ⓑ���ŕ\�����Ƃ��ł��܂��B
Ⓑ���́A�W����3���Ȃ̂ŁA�ő�v���[�g�d���A�ŏ��v���[�g�d���A�����ē����_�̒l��p���āA��Ɠ��l�Ɋe�W�������߂�ƁA
�ƂȂ�A �c�ݗ����v�Z���鎮��
�ł��B �܂��A���σv���[�g�d�����v�Z���鎮�́A
�ƂȂ�܂��B
���6V6�V���O���̃��[�h���C���ł̃v���[�g�d���̒l����❺���Řc�ݗ������߂�ƁA ��2�������g�c�ݗ�=5.4%�@ �ł����B ��3���ȍ~�̍����g�͖����Ɖ��肵�������ł����A��3���̍����g��5%���x�܂܂�Ă���g�`�ɂ�������炸�A�����l5.1%�Ɍ��\�Ƌ߂��l�������܂����B���܂��܂ł����ˁH
|
|
SYLVANIA���}�j���A���ɂ́A���[�h���C�������3���̍����g�c�ݗ������߂�v�Z�����L�ڂ���Ă��܂������A���̌����̋L�q�������A���́A�v�Z�ł���̂��s�v�c�ł����B �悤�₭���̗��������������Ƃ��́A�P���Ɋ����������ł��B�܂��A�����g�c�݂Ɋւ��đ̌n�I�ɗ������Ă��Ȃ����Ƃ��ǂ�������܂����B����web�ł�ǂ܂����͂���������Ȃ��Ǝv���܂������A�����̃m�[�g��ǂݕԂ��āA�������܂����B���A�{�e�́A�����g�c�݂����߂�d�g�݂���������ł����A�Ƃ�������̑厖�ȕ�����[�܂�����������܂��B
�Q�l���ЁF�u�d�q�lj�H�@S�E�V���\�� �}�R��O��v
|
�uKAKUSAN�^��ǃA���v�v�֖߂�@�@�@�@�u�^��ǃA���v�̘c���v�֖߂�
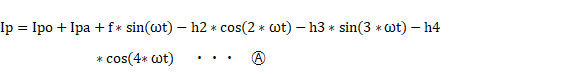
 �I������
�I������