|
�J�b�g�I�t���g�� |
��̍���̎��g�������}����AP-G�A�҂̍���̓����́A
Q �O�i�̏o�̓C���s�[�_���X��傫�����Ă��A����̓��������͌����Ȃ��B�t�ɁA�O�i�̏o�̓C���s�[�_���X�����������Ă��A����̓����͗lj����Ȃ��B
Q ���A�Ғ�R������������ƁA����̓����͗lj�����B
Q �܋Ɋǂ̓��͗e�ʂ͏��������߁A���A�Ғ�R�l��K�ɑI�ׂA����̓����͂��قLj������Ȃ��B
�Ɛ��@����܂����B
���̂��������H��p���Č����܂��B
�܂��A��̍�������̌v�Z���@�͎��g�����瑝���������߂���@�ł���A�_�C���N�g�ɃJ�b�g�I�t���g�����v�Z�ł��܂���B����́A�_�C���N�g�ɃJ�b�g�I�t���g���̒l���T�Z�ł��鎮�����߂܂��B
���ɂ������ẮA�ʏ�̑�����H�A�y�сAP-G�A�҂��{����������H�ł̃O���b�h�|�v���[�g�Ԃ̑�����Agp�́A
�E �ʏ�̑�����H��P-G�A�҉�H�ł́A���ق͖���
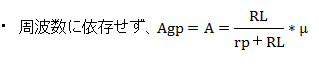
�ƌ��Ȃ����Ƃɂ��܂��B�i���̌��Ȃ���������A����グ�ł����B�B�B�@�u�O���b�h����v���[�g�܂ł̑������v���Q�Ɓ@�j�@�@
�ʏ��H�AP-G�A�҉�H�Ƃ��AAgp�����g�������������Ă��邽�߁A���͗e��Cs��Cin�{�iAgp+1�j*Cgp�́A���g���ɂ�荷�ق��o�܂��B���̂��߉�͂����G�ɂȂ�܂����A���̌��Ȃ��ɂ��A���g���ɂ��ϓ����Ȃ����A�Ƃ��Ĉ����A��͂��e�ՂɂȂ�܂��B
�|�@Cs=Cin+(Agp+1)*Cgp�@�ŁA���g���ɂ��ϓ��͂Ȃ�
�܂��A���̌��Ȃ��ɂ��A��H�S�̂̑������̕ω��ƁA���͂���O���b�h�܂ł̑������̕ω��������ƂȂ�̂ŁA���͂���O���b�h�܂ł̕ω���������������Ηǂ����ƂɂȂ�܂��B��̓I�ɂ́A�O���b�h�ɓ��͂����M���d���l�����͐M���d���l�̔����ƂȂ���g�����A�J�b�g�I�t���g���ɂȂ�܂��B
�ʏ��H�ł̃J�b�g�I�t���g��
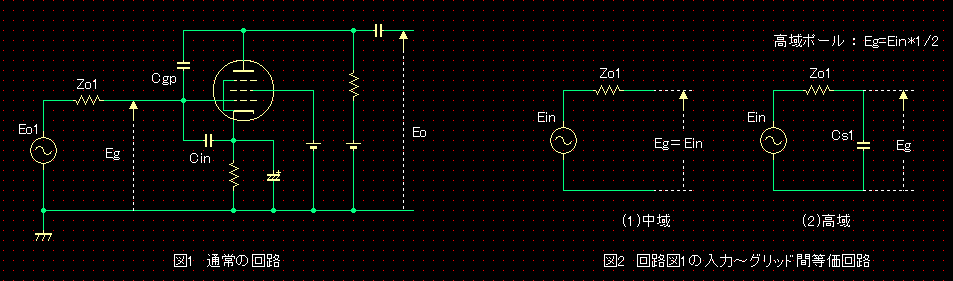
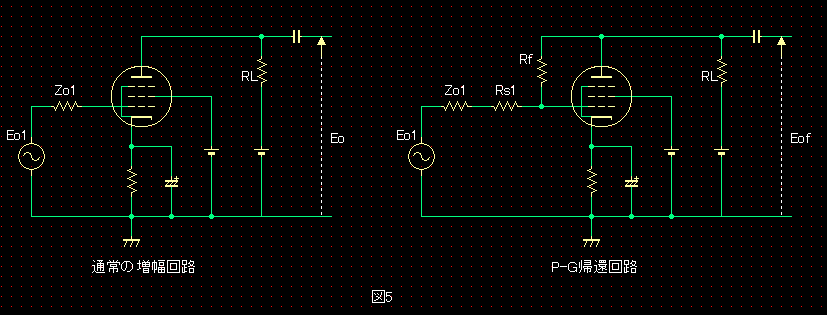
������ʏ�̉�H��}1�Ŏ����܂��B�O�i�̏o�̓C���s�[�_���X��Zo1�A�O���b�h�ƃv���[�g�ԁA�O���b�h�ƃJ�\�[�h�Ԃ̓d�Ɋԗe�ʂ����ꂼ��Cgp�ACin�Ƃ��Ė������Ă��܂��B
�}2�́A�}1�̉�H�̒���A�y�сA����ł̓��͂���O���b�h�܂ł̓�����H�ł��B����ł͓��͗e�ʂ͖����A�J�b�g�I�t���g���ł͓��͗e�ʂ�Cs1�Ƃ��Ă��܂��B
�@�@
�O���b�h�ɓ��͂����M���d���l�́A����ł͌�������Ein�̂܂܂ŁA�J�b�g�I�t���g���ł́A��̌��Ȃ��ɂ��A����̓d���l�̔����ɂȂ�܂��B
![]()
�]���A�J�b�g�I�t���g���ł̓��͗e��Cs1�̃��A�N�^���X�́A�O�i�̏o�̓C���s�[�_���XZo1�Ɠ������Ȃ�A�J�b�g�I�t���g���ł̓��͗e��Cs1�̃��A�N�^���X��Rcs1�A�J�b�g�I�t���g����Fp�Ƃ�����
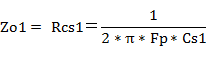
�ł��B
�ȏォ��A�ʏ�̉�H�ł̃J�b�g�I�t���g�����@
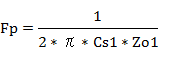
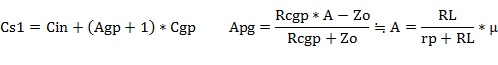
�ƂȂ�܂����B
P-G��H�ł̃J�b�g�I�t���g��
���́AP-G�A�҉�H�i�}3�j���������܂��B
�}4�́A��H�}3�̒���A�y�сA����ł̓��͂���O���b�h�܂ł̓�����H�ł��B����ł͓��͗e�ʂ͖����A�J�b�g�I�t���g���ł͓��͗e�ʂ�Cs2�Ƃ��Ă��܂��B
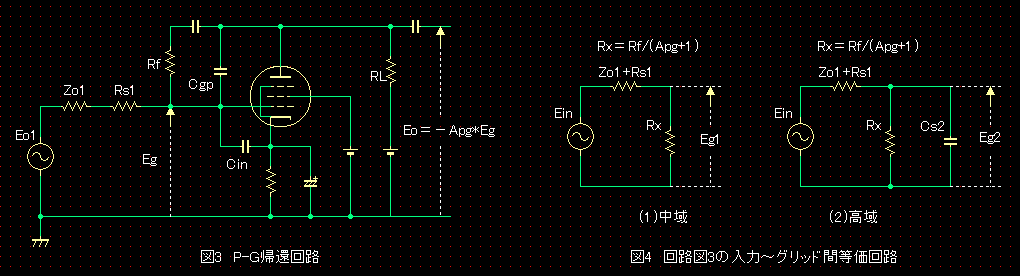
�O���b�h����v���[�g�Ԃ̑�������Agp�Ƃ���ƁA�v���[�g�ɂ̓O���b�h�d��Eg�́|Agp�{�̐M���i�𗬓d���j������܂��B
Rf1�́A�O���b�h�����猩��ƁA�v���[�g���̓d�ʂ�Eo=�|Agp*Eg�Ȃ̂ŁA�l���i1+Agp�j���̂P�{�̑傫���ŃO�����h�ɒ��ڗ������R�Ƃ݂Ȃ��܂��B
Rx=Rf/(Agp+1)
�J�b�g�I�t���g���ł́A�O���b�h�d��������ł̃O���b�h�d���̔����Ɍ��������̂ŁA���͗e��Cs2�̃��A�N�^���X��Rcs2�A�J�b�g�I�t���g����Fpf �Ƃ�����
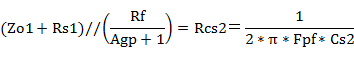
�ό`��(#1)�A P-G�A�҉�H�ł̃J�b�g�I�t���g�������߂��
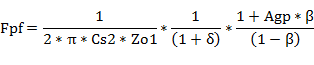
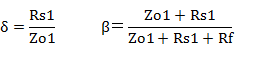
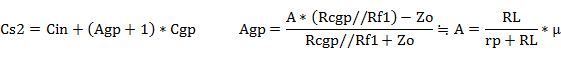
�܂Ƃ�
![]()
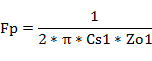
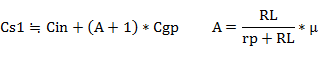
P-G�A�҉�H�ł̃J�b�g�I�t���g��Fpf�́A
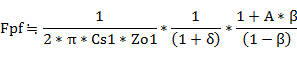
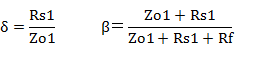
�]���AP-G�A�҉�H�ł̃J�b�g�I�t���g��Fpf�́A

�ȏォ��A�ʏ�̑�����H��P-G�A�҂��{���ƁA�J�b�g�I�t���g��Fp�́A

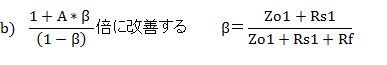
�ƂȂ�܂����B
�@��ό`�����(#2)
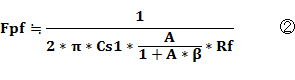
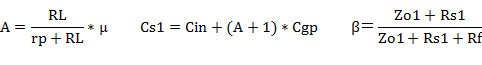
�A������AP-G�A�҉�H�ł́A����̕��A�җʁi�P�{A*���j�Ŕ�ׂ��ꍇ
Q �O�i�̏o�̓C���s�[�_���X��傫�����Ă��A����̓��������͌����Ȃ��B�t�ɁA�O�i�̏o�̓C���s�[�_���X�����������Ă��A����̓����͗lj����Ȃ��B
Q ���A�Ғ�R������������ƁA����̓����͗lj�����B
Q �܋Ɋǂ̓��͗e�ʂ͏��������߁A���A�Ғ�R�l��K�ɑI�ׂA����̓����͂��قLj������Ȃ�
�������邩�Ǝv���܂�
�J�b�g�I�t���g���Z�o��
�A���������₷���P�ʂɂ���Ɓi�邯����̃C���s�[�_���X�����܂˂Ă݂܂����B�j

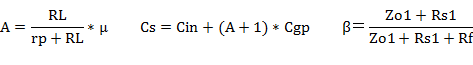
�ƂȂ�܂��B
P-G�A�҂ł̃J�b�g�I�t���g���̊T�Z�l����y�Ɍv�Z�ł��邩�Ǝv���܂��B�ÎZ�͖������Ȃ��B�B�B
���̃J�b�g�I�t���g���T�Z�������Z���Ă݂܂�
��̍�������}��`����EL34��3���̃P�[�X���ɂ��܂��B�g�ڍׂȌv�Z�g��6.2�̌v�Z���ɂ��l�A�h�ȈՌv�Z�h�́g�J�b�g�I�t���g���T�Z���h �ɂ��l�ł��B
�l�͂قڈ�v���Ă���A1MHz�܂ł͂ǂ����Ǝv���܂����A����Ȃ�Ɏg����̂ł͂Ȃ��ł��傤���B

�⑫
#1�@�ό`�ߒ�
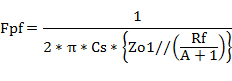
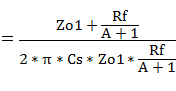
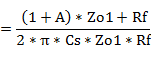
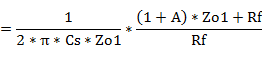
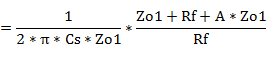
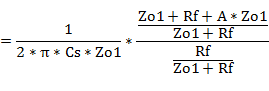
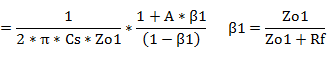
#2�@�ό`�ߒ�

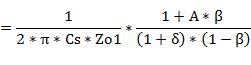
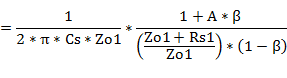
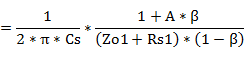
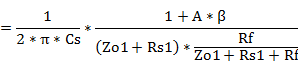
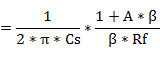
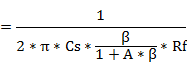
�uKAKUSAN�^����A���v�v�֖߂�@�@�@�u���̕ł̃g�b�v�v�֖߂�