P-G帰還を施した増幅回路における高域での増幅率の計算式を等価回路を用いて求めてみます。
図1が検討対象としたP-G帰還回路です。高域特性を左右する“見えないコンデンサーのCgpとCinを明示しました。また、前段の出力インピーダンスをZo1、信号電圧をEo1としています。
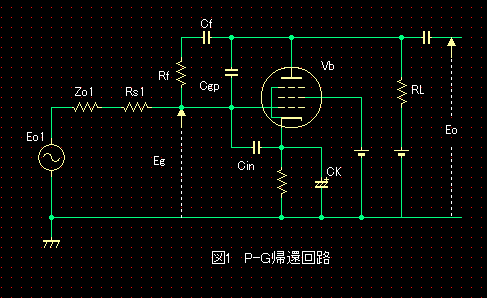
P-G帰還回路の高域での増幅率
図1の等価回路が図2です。(1)ではCgpとCinのリアクタンスをRcgp、Rcinとし、また、Ck、Cfは短絡しました。(2)は、(1)の素子数を削減して簡素化した等価回路です。
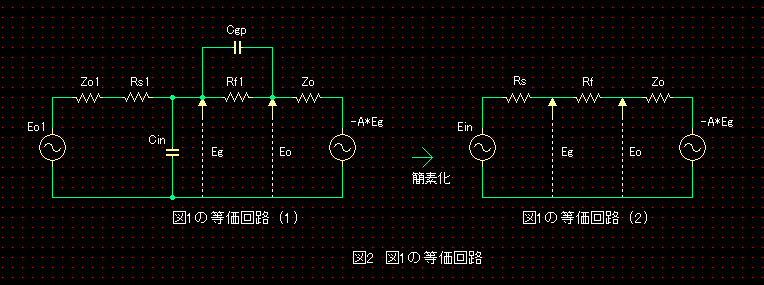
図2において、Zo、A、Ein、Rs、Rfは、以下となります。 μ、及び、rpは、ベース管Vbの増幅率と内部抵抗です。
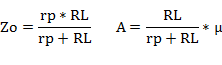
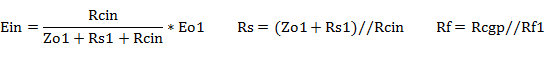
こうして素子数を減らした図2(2)の等価回路は、P-G帰還回路の等価回路そのものになりました。これにより、高域になると表れる(存在を計算に入れる必要性がでる)CgpとCinは、P-G帰還としての振る舞い自体を変えることは無く、負帰還抵抗Rs、Rfの値や帰還率βの値を変化させる作用があることが判ります。
別な表現では、P-G帰還回路では、電極間の容量に配慮すると、負帰還抵抗Rs、Rfは、Rs=Zo1+Rs1からRs=(Zo1+Rs1)//Rcin、また、Rf=Rf1からRf=Rcgp//Rf1 となります。
例えば、Zo1=30KΩ、Rs1=70KΩ、Rf1=900KΩとした場合、電極間容量を気にしないと、Rs=100KΩ、Rf=900KΩで、帰還量β(=Rs/(Rs+Rf) は 0.1です。ここで、EL34の電極間容量は、Cin=15.2pF、Cgp=1pFですが、この電極間容量に配慮すると、1KHz、100KHz、300KHzでの帰還量β(=Rs/(Rs+Rf)、及び、Rs、Rf は以下となり、高域での振る舞いに変化を与えることが明らかです。
|
周波数 |
β |
Rs |
Rf |
|
1KHz |
0.10 |
99KΩ |
895KΩ |
|
100KHz |
0.08 |
51KΩ |
575KΩ |
|
300KHz |
0.07 |
26KΩ |
334KΩ |
図1のP-G帰還回路の入力から出力までの増幅率の算出式を求めます。図2(2)の回路のEinからEoまでの増幅率の算出式は、「6.1 等価回路による増幅率の算出」によると、以下でした。
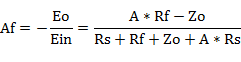
従い、
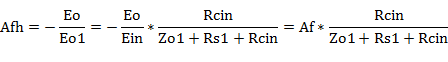
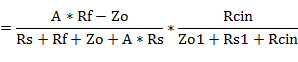
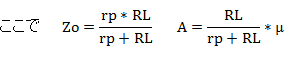
![]()
となります。
同様に、図2(2)の回路のグリッドからプレートまでの増幅率は、
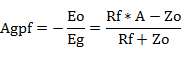
でしたので、図1のP-G帰還回路のグリッドからプレートまでの増幅率は、
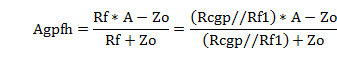
となります。
通常の増幅回路の高域の増幅率
比較検討のため、P-G帰還を施していない通常の増幅回路の高域での増幅率の計算式を求めてみます。
図3が、検討対象とした通常の増幅回路です。図1の回路からRs1、Rf1を削除した回路です。また、高域特性を左右する“見えないコンデンサー”のCgpとCinを明示しました。
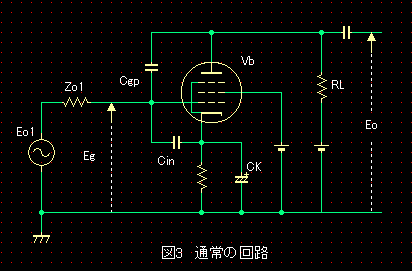
図3の等価回路が図4です。図2と同様に、CgpとCinのリアクタンスをRcin、Rcgpとして素子数を削減した等価回路が(2)です。
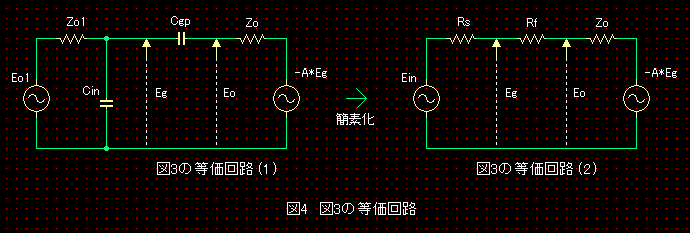
こうして図にして理解できたのですが、CgpとZo1&Cinって、負帰還抵抗のRfとRsに相当しますよね。
つまり、無負帰還の増幅回路でも、高域ではP-G帰還と同じくプレートからグリッドに負帰還がかかっている! ということになります。
ということで、通常の増幅回路の高域の特性の計算も、P-G帰還回路の増幅率を活用します。
図4において、Zo、A、Ein、Rs、Rfは、以下となります。 μ、及び、rpは、ベース管Vbの増幅率と内部抵抗です。
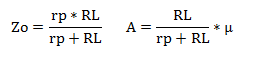
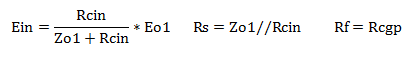
図4(2)の等価回路は、P-G帰還回路等価回路そのものです。従い、通常の回路での高域での増幅率は、
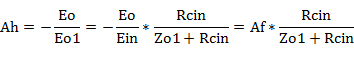
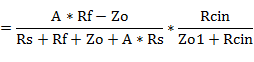
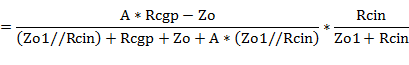
となります。
さらに、通常の回路の高域のグリッドからプレートまでの増幅率は
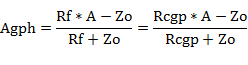
となります。
以上により、高域での増幅率が計算できるようになりました。
まとめ
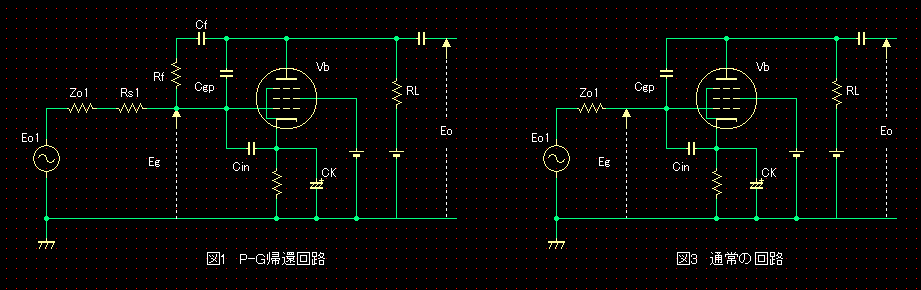
図1のP-G帰還回路での高域の増幅率Afh、また、高域のグリッドからプレートまでの増幅率Agpfhは
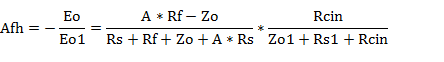
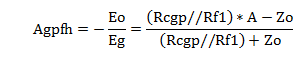
図3の通常の回路での高域の増幅率Ah、また、高域のグリッドからプレートまでの増幅率Agphは
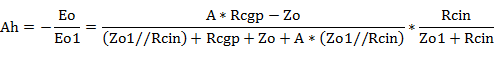
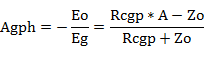
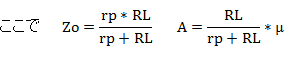
感想
通常回路での入力容量の作用が、P-G帰還回路と同じメカニズムとは意外でした。
「KAKUSANアンプ」へ戻る 「この頁のトップ」へ戻る