2次歪みの打ち消しの塩梅をシミレーションしていたら、3次歪みが増加していることに気がつきました。何故なんでしょうか。
3次歪みの波形
真空管の増幅回路で発生する3次歪みの波形(3次高調波)は、出力信号の基本波(歪みなく増幅された波形)に対して、周波数は3倍で、位相は180度の差があるそうです。
前項の2次歪みの波形の検討と同様に3次歪みの波形と入力波形の関係を求めてみます。
入力信号(5周期分のサイン波)とその出力信号の基本波と3次高調波を表してみました。360度(1周期)毎に90度の間隔で4区間に区分しています。
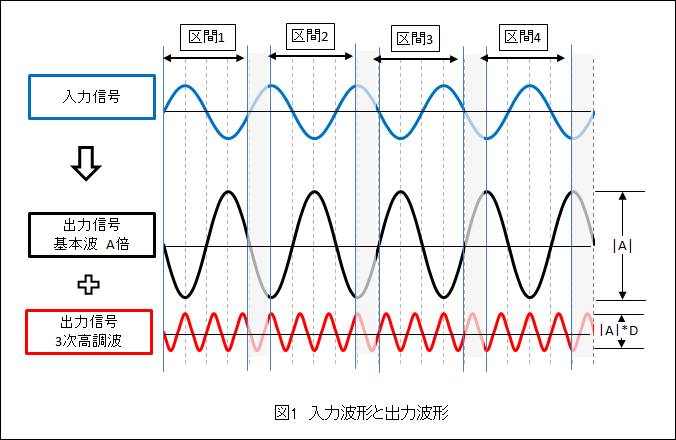
1周期分の波形にはサイン波、コサイン波、マイナスのサイン波、マイナスのコサイン波の4種類があります。各区間の入力波形は、この4種類のいずれかに相当します。それぞれを入力したときの出力(基本波と2次高調波、3次高調波の波形の組み合わせ)を図1から読み取り、表1にまとめてみました。例えば、区間1は入力波形がサイン波のときですが、入出力で正負が反転するので、出力される基本波はマイナス・サイン波で、2次高調波(歪み成分)はマイナ・スコサイン波、3次高調波はマイナス・サイン波になります。増幅率をA倍、2次高調波率をD2%、3次高調波率をD3%としています。
|
入力波形(1周期) |
出力波形 (基本波と2次、3次高調波) |
|||
|
区間1 |
サイン波 |
k*sin(θ) |
基本波 |
-A*k*sin(θ) |
|
2次高調波 |
-A*D2*k*cos(2*θ) |
|||
|
3次高調波 |
-A*D3*k*sin(3*θ) |
|||
|
区間2 |
コサイン波 |
k*cos(θ) |
基本波 |
-A*k*cos(θ) |
|
2次高調波 |
A*D2*k*cos(2*θ) |
|||
|
3次高調波 |
A*D3*k*cos(3*θ) |
|||
|
区間3 |
マイナス・サイン波 |
-k*sin(θ) |
基本波 |
A*k*sin(θ) |
|
2次高調波 |
-A*D2*k*cos(2*θ) |
|||
|
3次高調波 |
A*D3*k*sin(3*θ) |
|||
|
区間4 |
マイナス・コサイン波 |
-k*cos(θ) |
基本波 |
A*k*cos(θ) |
|
2次高調波 |
A*D2*k*cos(2*θ) |
|||
|
3次高調波 |
-A*D3*k*cos(3*θ) |
|||
表1 入力波形と出力波形の関係(A:増幅率、D2:2次高調波率、D3:3次高調波率)
3次歪みの様子
初段と終段から成る2段アンプの2次歪みの打ち消しの様子を信号の波形から調べてみます。初段、終段の増幅率をそれぞれA1、A2、2次高調波率をそれぞれ、D12、D22、3次高調波率をそれぞれ、D13、D23、とします。
ますは初段です。
表1から、初段にサイン波(k*sin(θ))を入力したとき、基本波①、2次高調波②と3次次高調波③が出力されます。
|
初段入力 |
初段出力 |
||
|
サイン波 |
① |
基本波 |
-A1*k*sin(θ) |
|
② |
2次高調波 |
-A1*D12*k*cos(2*θ) |
|
|
③ |
3次高調波 |
-A1*D13*k*sin(3*θ) |
|
表2 初段の入力と出力
次は終段です。
上記の初段の3ヶの出力波形①と②と③が終段に入力されます。①、②、③は、個々に歪みの無い波形であり、①、②、③の入力に対応して基本波と2次高調波と3次高調波が出力されます。④は歪みの無い信号で、⑤から⑫が元の信号には無い歪み成分です。
|
終段入力 |
終段出力 |
|||
|
① |
マイナス・サイン波 |
④ |
①の基本波 |
A2*A1*k*sin(θ) |
|
⑤ |
①の2次高調波 |
-A2*D22*A1*k*cos(2*θ) |
||
|
⑥ |
①の3次高調波 |
A2*D23*A1*k*sin(3*θ) |
||
|
② |
マイナス・コサイン波 |
⑦ |
②の基本波 |
A2*A1*D12*k*cos(2*θ) |
|
⑧ |
②の2次高調波 |
A2*D22*A1*D12*k*cos(4*θ) |
||
|
⑨ |
②の3次高調波 |
-A2*D23*A1*D12*k*cos(6*θ) |
||
|
③ |
マイナス・サイン波-A1*D13*k*sin(3*θ) |
⑩ |
③の基本波 |
A2*A1*D13*k*sin(3*θ) |
|
⑪ |
③2次高調波 |
-A2*D22*A1*D13*k*cos(6*θ) |
||
|
⑫ |
③の3次高調波 |
A2*D23*A1*D13*k*sin(9*θ) |
||
表3 終段の入力と出力
表3のままでは判り難いので周波数毎に分類してみました。
|
終段出力 |
||
|
基本波 |
④ |
A2*A1*k*sin(θ) |
|
2次高調波 |
⑤+⑦ |
(D12-D22)*A2*A1*k*cos(2*θ) |
|
3次高調波 |
⑥+⑩ |
(D13+D23)*A2*A1*k*sin(3*θ) |
|
4次高調波 |
⑧ |
D22*D12*A2*A1*k*cos(4*θ) |
|
6次高調波 |
⑨+⑪ |
-(D23*D12+D22*D13)*A2*A1*k*cos(6*θ) |
|
9次高調波 |
⑫ |
D23*D13*A2*A1*k*sin(9*θ) |
表4 終段出力の基本波と高調波
表4から明らかなように、3次歪みの⑥と⑩は打ち消されず加算されて、歪み率は (D13+D23)*A1*A2 となることが判りました。
また、4次高調波、6次高調波、9次高調波が2段化により新たに生成されることが判りました。
「KAKUSAN真空管アンプ」へ戻る 「この頁のトップ」へ戻る