2���c�݂̑ł�������_�����V���O���E�A���v�̐v������ꍇ�A�Ⴆ�ΏI�i�̘c�ݗ���5%�������Ƃ��āA�O�i�̘c�ݗ��͂ǂ̂��炢�̉��~���ǂ��̂ł��傤���B���o�I�ɂ́A�����c�ݗ���5%���ǂ������Ǝv���܂����A�ǂ��Ȃ̂ł��傤���H�@�܂��A�c�ݗ��ɈႢ���������Ƃ��̓A���v�S�̂ł͂ǂ̒��x�̘c�ݗ��ɂȂ�̂ł��傤���B�o�͂��傫���Ƙc�ݗ��������Ȃ�̂ŁA���������W����̂ł��傤���B
���̂������T�K���Ă݂܂����B
�Q���c�݂̔g�`
�����g�������ۂɕ\���2���c�݁i2�������g�j�̔g�`�́A�ʔ������Ƃɘc�݂̂Ȃ����ꂢ�Ȑ����g�Ȃ̂������ł��B�������A��{�g�i�c�݂Ȃ��������ꂽ�g�`�j�ɑ��āA���g����2�{�ŁA�ʑ���90�x�̍������邻���ł��BSin(���j�� A�{�ɑ��������ꍇ�̊�{�g�Ɗ�{�g��D%�̔g����2�������g���P�����������G�N�Z�����g���ăO���t�����Ă݂܂����B
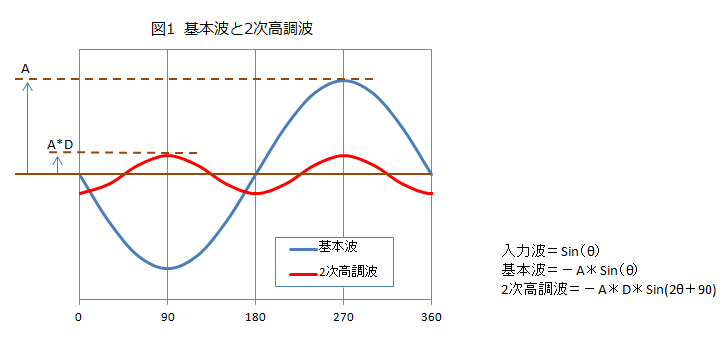
�����l�ɁA���͐M���i5�������̃T�C���g�j�Ƃ��̏o�͐M���̊�{�g��2�������g���O���t�ŕ\���Ă݂܂����B�^��ǃA���v�������ΏۂȂ̂ŏo�͂�180�x���]�����Ă��܂��B�܂��A360�x�i1�����j����90�x�̊Ԋu��4��Ԃɋ敪���Ă��܂��B
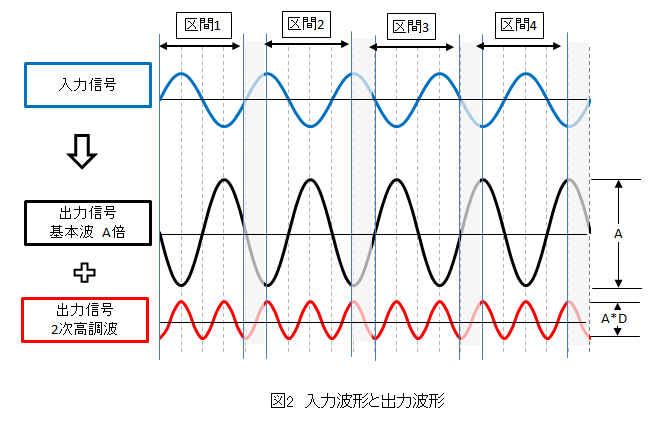
1�������̔g�`�ɂ̓T�C���g�A�R�T�C���g�A�}�C�i�X�̃T�C���g�A�}�C�i�X�̃R�T�C���g��4��ނ�����܂��B�e��Ԃ̓��͔g�`�́A����4��ނ̂����ꂩ�ɑ������܂��B���ꂼ�����͂����Ƃ��̏o�́i��{�g��2�������g�̔g�`�̑g�ݍ��킹�j���A�}2����ǂݎ��A�\�P�ɂ܂Ƃ߂Ă݂܂����B�Ⴆ�A���1�ł͓��͔g�`���T�C���g�ł���A�o�͂�����{�g�̓}�C�i�X�E�T�C���g�A2�������g�̓}�C�i�X�E�R�T�C���g�ɂȂ�܂��B��������A�{�A2�������g����D%�Ƃ��Ă��܂��B
|
���͔g�`�i1�����j |
�o�͔g�`�@�@�i��{�g��2�������g�j |
|||
|
���1 |
�T�C���g |
k*sin(��) |
��{�g |
-A*k*sin(��) |
|
2�������g |
-A*D*k*cos(2*��) |
|||
|
���2 |
�R�T�C���g |
k*cos(��) |
��{�g |
-A*k*cos(��) |
|
2�������g |
A*D*k*cos(2*��) |
|||
|
���3 |
�}�C�i�X�E�T�C���g |
-k*sin(��) |
��{�g |
A*k*sin(��) |
|
2�������g |
-A*D*k*cos(2*��) |
|||
|
���4 |
�}�C�i�X�E�R�T�C���g |
-k*cos(��) |
��{�g |
A*k*cos(��) |
|
2�������g |
A*D*k*cos(2*��) |
|||
�\1�@���͔g�`�Əo�͔g�`�̊W�i��������A�A2�������g�c�ݗ���D�j
���̕\1���g����2���c�݂̑ł������̗l�q�ׂĂ݂܂��B���͔g�`���T�C���g�ƃR�T�C���g�Ƃŕ����Ă݂��Ƃ��낪�~�\���Ǝv���Ă܂��B
2���c�݂̑ł������̗l�q
���i�ƏI�i���琬��2�i�A���v��2���c�݂̑ł������̗l�q��M���̔g�`���璲�ׂĂ݂܂��B���i�ƏI�i�̑�������2�������g�����A���ꂼ��AA1�AD1�AA2�AD2�Ƃ��܂��B
�܂��͏��i�ł��B
�\1����A���i��k�{���T�C���g�ik*sin(��)�j�̐M�������͂����Ƃ��AA1�{�ɑ������ꂽ�c�݂̖�����{�g�@�ƁA�U������{�g�@��D1%�ł���2�������g�A���o�͂���܂��B
|
���i���� |
���i�o�� |
||
|
�T�C���g |
�@ |
��{�g |
-A1*k*sin(��)�@ |
|
k*sin(��) |
�A |
2�������g |
-A1*D1*k*cos(2*��) |
�\2�@���i�̓��͂Əo��
���͏I�i�ł��B
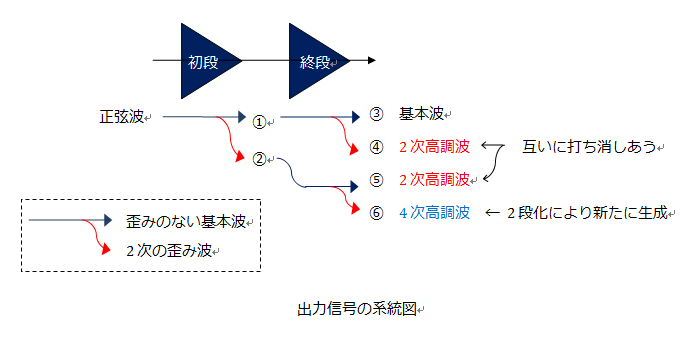
�I�i�̓��͐M���́A��L�̏��i�̏o�͂ł����{�g�@��2�������g�A�ɂȂ�܂��B�A�͏��i�̘c�ݐ����ł����A�P�Ƃ̔g�`�Ō���A�c�݂̖����Y��Ȑ����g�ł��B�]���āA�@�̏o�͂Ƃ��Ċ�{�g�B��2�������g�C�������悤�ɁA�A�̏o�͂Ƃ��Ċ�{�g�D��2�������g�E���o�͂���܂��B�@�̓}�C�i�X�E�T�C���g�A�A�̓}�C�i�X�E�R�T�C���g�ł��̂ŁA�\1����A�C����E�̔g�`�����߂�ƁA�\3�̂悤�ɂȂ�܂��B
|
�I�i���́i=���i�o�́j |
�I�i�o�� |
|||
|
�@ |
�}�C�i�X�E�T�C���g |
�B |
�@�̊�{�g |
A2*A1*k*sin(��) |
|
-A1*k*sin��) |
�C |
�@��2�������g |
-A2*A1*D2*k*cos(2*��) |
|
|
�A |
�}�C�i�X�E�R�T�C���g |
�D |
�A�̊�{�g |
A2*A1*D1*k*cos(2*��) |
|
-A1*D1*k*cos(2*��) |
�E |
�A��2�������g |
A2*D2*A1*D1*k*cos(4*��) |
|
�\3�@�I�i�̓��͂Əo��
�o�͐M���́A�B�����E��4���̔g�`�����Z���ꂽ�g�`�ł��B�A���v�S�̂��猩��A�B�͘c�ݖ����������ꂽ�o�͐M���i��{�g�j�ŁA�C�A�D�A�E���c�ݐ����i�����g�j�ł��B
�o�͐M�����B+�C+�D�{�E
�@�B�E�E�E�c�݂Ȃ��������ꂽ��{�g
�C�A�D�A�E�E�E�E�c�ݐ���
�����ŁA�c�ݐ����C���D�͊�{�g��2�{�̎��g���̔g�`��2�������g�ł��B�C�A�D�́A������g���Ő����̔g�`�Ȃ̂ʼn��Z����ƌ݂��ɑł����������܂��B�����āA���i�ƏI�i�̘c�ݗ����������Ƃ��iD1=D2�̂Ƃ��j�ɁA���S�ɑł�������邱�Ƃ�����܂��B
2���c�݁��C+�D��(D1-D2)*A1*A2*k*cos(2*��)
�C�́A�I�i�Ŕ�������c�ݐ����ŁA�D�͏��i�Ŕ�������c�ݐ����ł��B���i�Řc�݂Ȃ��������ꂽ�M���i��{�g�j���I�i�ő������ꂽ�ۂɔ�������2���c���C�ƁA���i�Ŕ�������2���c�ݐ������I�i�Řc�ނ��ƂȂ��������ꂽ�D�Ƃ��A�݂��ɑł����������킯�ł��B
���ꂪ�A2�i�A���v�ł�2���c�݂̑ł������A�̐��̂ł͂Ȃ��ł��傤���B
���ɁA�E����A2�i���������Ƃɂ��A�V����4�������g�i4���c�݁A�c�ݗ���D1*D2�j���������Ă��邱�Ƃ�����܂��B2���c�݂̑ł�������100%�ł��āA�C�{�D��0 �ƂȂ����Ƃ��Ă��A�o�͔g�`�ɂ́A2�i���ɂ��V���ɔ��������c�ݐ������E���c��܂��B
�E ��A2*A1*D2*D1*k*cos(4*��)�E�E�E�V���ɐ������ꂽ4���c��
�ȏォ��A
���ʓI��2���c�݂̑ł�������_�����v��@�Ƃ��ẮA�K��d�����A���v����o�͂����Ƃ��̏��i��2���c�ݗ�D1 �ƏI�i��2���c�ݗ�D2 ���������Ȃ�悤�ɐv����Ηǂ��A�Ƃ������ƂɂȂ�܂����B���_�I�ɂ́AD1=D2 �̂Ƃ���2���c�݂͊��S�ɖ����Ȃ�AD1��D2 �̂Ƃ��� |D1�|D2| �̗ʂ�2���c�݂��c��܂��B
�܂��A2�i���������Ƃɂ��V����4���c�݂��������A���̘c�ݗ��� D1*D2 �ł��B�Ⴆ�AD1=10%�AD2=11% �̏ꍇ�A�i3���ȍ~�̘c�݂͖����Ƃ��āj�A�A���v�S�̂�2���c�ݗ��� 1% �ƂȂ�A4���c�ݗ��� 1.1% �ƂȂ�܂��B
2���c�݂̑ł����������Ƃ��ẮA���i�ƏI�i�̑������͊W������܂���ł����B
�܂��A���o�͂̔g�`���t�]���Ȃ��ƁA2���c�݂͑ł������ꂸ�A�t�ɉ��Z����A�c�ݗ��� D1+D2 �ɂȂ�܂��B
�g�`�̎��o�I�ȃA�v���[�`�ŃX�}�[�g�Ȃ����ł͖��������ł����A�ł������̗l�q���͂߂܂����B
�Q�l�������y�[�W
�邯����@�u���̃A���v�v�}�j���A�� / �^��ǂŔ�������c��(���A�҂̗\���m��)�v
EDN Japan����@ EDN Japan >�A�i���O >�f�W�^���I�[�f�B�I�̊�b���牞�p�i3�j
Wikipedia�����@�S�����g�c
�uKAKUSAN�^����A���v�v�֖߂�@�@�@�u���̕ł̃g�b�v�v�֖߂�